What will you learn from this slecture?

• A toy example of using PCA to gain some intuition behind the method
• The mathematical reasoning behind this approach
• The strength and limitation of PCA and potential working field

Prerequisite

This tutorial only requires a working knowledge of baisc linear algebra. If you are familar with standard deviation, covariance and eigen decompostion, then you are fine. If not, Gilbert Strang wrote a great book^[1], which is of great help.

Introduction

Principle Component Analysis (PCA) is a statistical method that uses orthonormal transformations to convert the observed correlated data into a set of linearly uncorrelated data, which are the so-called principle components. PCA has found numerous application fields like face recognition, dimension reduction, factor analysis and image compression, etc. Generally speaking, it's a common technique that can find certain patterns in high-dimension data, and thus can reduce the computation efforts by only considering a certain set of significant patterns. When dealing with high-dimension data, it's always not easy for us to visualize the distribution of data, and thus it's very hard to find certain patterns from data which could lead to a better desigh of classifier. PCA could help us in this case, to find the significant patterns. 

This tutoril is divided into three sections

1. A toy example
2. Mathematical derivation
3. Discusssion

A toy example

In this section, I will just use PCA on a simple data set to helo you gain some intuition of PCA, the question of "why does it work" is not answered in this section, we just focus on "how to make it work". Then after you get enough intuition from this toy example, you can decide whether PCA will work fine in your application scenario. The mathematical derivation will come later.

There are basically 6 steps in the procedure of using PCA, they are 1) Construct the data set, 2) Subtract the mean, 3) Calculate the covariance matrix, 4) Get eigen decomposition of covariance matrix, 5) Choose the significant principle components, 6) Get the transformed data. Now we will go through all of them in detail.

Step1: Construct the data set

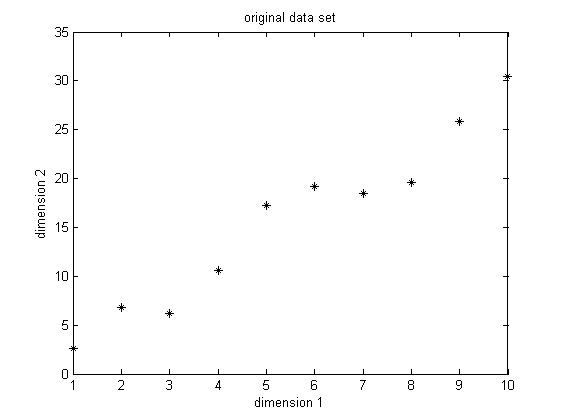
The data set I choose is only two dimension, because it's easier for visualization. The original data set is shown below in Figure1. This is only a made-up data, there are 10 observations. As we can easily find, there is a positive correlation between the two dimensions. 

                                               Figure 1. Original data set, data dimension is 2, 10 observations

Step2: Subtract the mean
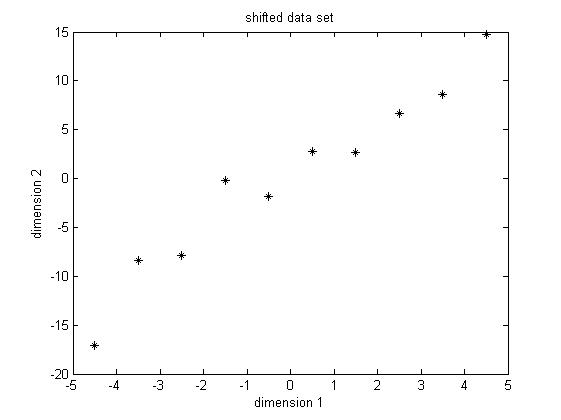
PCA requires the data set to have zero mean in each of the dimensions so that it can work properly. Thus we have to subtract the mean, which is the sample average, in each dimension. It's not hard to find out that the sample average for the data in dimension 1 is 5.5 and that for dimension 2 is 15.5. Then for data in each dimension, we subtract the correponding mean, the result shifted data is shown in Figure 2.  

                                      Figure 2. Shifted data set, subtract the sample average for each dimension

Step3: Calculate the covariance matrix Since the data is two-dimensional, the covariance matrix should be a symmetric 2x2 matrix. The formula to calculate covariance is $ \sigma_(x,y) = \textbf{E}[(x-\textbf{E}(x))(y-\textbf{E}(y))] $  

References

1. Gilbert Strang, "Introduction to Linear Algebra", Wellesley-Cambridge Press, February 2009. ISBN: 9780980232714
2. Mireille Boutin, "ECE662: Statistical Pattern Recognition and Decision Making Processes," Purdue University, Spring 2014.

Questions and comments

If you have any questions, comments, etc. please post them on this page.