Jacobians and their applications

by Joseph Ruan

Basic Definition

The Jacobian Matrix is just a matrix that takes the partial derivatives of each element of a transformation. In general, the Jacobian Matrix of a transformation F, looks like this:

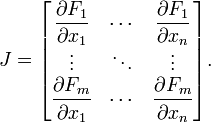F₁,F₂, F₃... are each of the elements of the output vector and x₁,x₂, x₃ ... are each of the elements of the input vector.

So for example, in a 2 dimensional case, let T be a transformation such that T(u,v)=<x,y> then the Jacobian matrix of this function would look like this:

$ J(u,v)=\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix} $

This Jacobian matrix noticably holds all of the partial derivatives of the transformation with respect to each of the variables. Therefore each row contains how a particular output element changes with respect to each of the input elements. This means that the Jacobian matrix contains vectors that help describe how a change in any of the input elements affects the output elements.

To help illustrate making Jacobian matrices, let's do some examples:

Example #1:

What would be the Jacobian Matrix of this Transformation?

$ T(u,v) = <u*\cos v, u*\sin v> $ .

Solution:

$ x=u*\cos v \longrightarrow \frac{\partial x}{\partial u}= \cos v , \; \frac{\partial x}{\partial v} = -u*\sin v $

$ y=u*\sin v \longrightarrow \frac{\partial y}{\partial u}= \sin v , \; \frac{\partial y}{\partial v} = u*\cos v $

$ J(u,v)=\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{bmatrix}= \begin{bmatrix} \cos v & -u*\sin v \\ \sin v & u*\cos v \end{bmatrix} $

This example actually showcased the transformation "T" as the change from polar coordinates into Cartesian coordinates.

Example #2:

What would be the Jacobian Matrix of this Transformation?

$ T(u,v) = <u, v, u^v>,u>0 $ .

Solution:

Notice, that this matrix will not be square because there is a difference in dimensions of the input and output, i.e. the transformation is not injective.

$ x=u \longrightarrow \frac{\partial x}{\partial u}= 1 , \; \frac{\partial x}{\partial v} = 0 $

$ y=v \longrightarrow \frac{\partial y}{\partial u}=0 , \; \frac{\partial y}{\partial v} = 1 $

$ z=u^v \longrightarrow \frac{\partial y}{\partial u}= u^{v-1}*v, \; \frac{\partial y}{\partial v} = u^v*ln(u) $

$ J(u,v)=\begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} \end{bmatrix}= \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ u^{v-1}*v & u^v*ln(u)\end{bmatrix} $

Example #3:

What would be the Jacobian Matrix of this Transformation?

$ T(u,v) = <\tan (uv)> $ .

Solution:

Notice, that this matrix will not be square because there is a difference in dimensions of the input and output, i.e. the transformation is not injective.

$ x=\tan(uv) \longrightarrow \frac{\partial x}{\partial u}= \sec^2(uv)*v, \; \frac{\partial x}{\partial v} = sec^2(uv)*u $

$ J(u,v)= \begin{bmatrix}\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \end{bmatrix}=\begin{bmatrix}\sec^2(uv)*v & sec^2(uv)*u \end{bmatrix} $

Application: Jacaobian Determinants

The determinant of Example #1 gives:

$ \left|\begin{matrix} \cos v & -u * \sin v \\ \sin v & u * \cos v \end{matrix}\right|=~~ u \cos^2 v + u \sin^2 v =~~ u $

Notice that, in an integral when changing from cartesian coordinates (dxdy) to polar coordinates $ (drd\theta) $, the equation is as such:

$ dxdy=r*drd\theta=u*dudv $

It is easy to extrapolate, then, that the transformation from one set of coordinates to another set is merely

$ dC1=det(J(T))dC2 $

where C1 is the first set of coordinates, det(J(C1)) is the determinant of the Jacobian matrix made from the Transformation T, T is the Transformation from C1 to C2 and C2 is the second set of coordinates.

It is important to notice several aspects: first, the determinant is assumed to exist and be non-zero, and therefore the Jacobian matrix must be square and invertible. This makes sense because when changing coordinates, it should be possible to change back.

Moreover, recall from linear algebra that, in a two dimensional case, the determinant of a matrix of two vectors describes the area of the parallelogram drawn by it, or more accurately, it describes the scale factor between the unit square and the area of the parallelogram. If we extend the analogy, the determinant of the Jacobian would describe some sort of scale factor change from one set of coordinates to the other. Here is a picture that should help:

This is the general idea behind change of variables. It is easy to see for the one dimensional case that for

$ T(u)=u^2=x ~~, $$ ~~~~~~~~ J(u)=\begin{bmatrix}\frac{\partial x}{\partial u}\end{bmatrix}=\begin{bmatrix}2u\end{bmatrix} $$ ,~~~~~~~ dx=\left|J(u)\right|*du=2u*du $ And thus, we get the same derivation of change of variables for the one dimensional case. Let's do some examples:

Example #4:

Sources:

1. [[1]]