The question stated:
2. Use Matlab to demonstrate summing of a finite number of terms of a Fourier Series ... pick a fun time function with a discontinuity to illustrate Gibbs phenomena. How does the Gibbs overshoot behave as the number of terms in the FS increases?
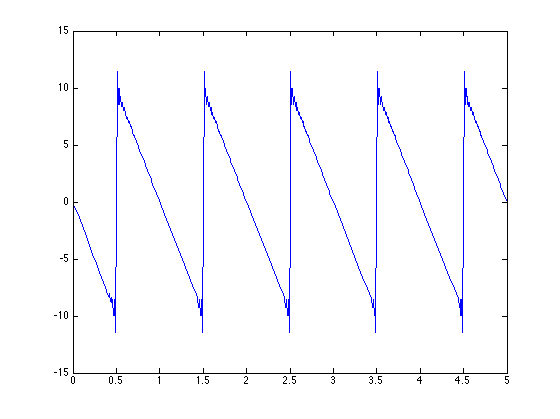
The function chosen was a sawtooth wave with frequency 1.
k = 5
k = 10
k = 25
k = 50
k = 100
As the number of terms in the FS increased the overshoot became more pronounced around k = 25, but around k = 100 it smoothed out and adhered more to the look of a sawtooth wave.