problem solving
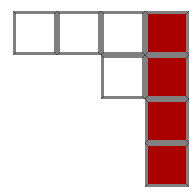
You are in the middle of a Tetris game and you have two pieces left until proceeding to the next level. The board currently looks like this:

Your goal is to complete the four rows with the last two Tetris pieces. The seven available Tetris pieces are shown below. What are your chances of completing the four rows in the next two turns? It should be noted that the pieces can be rotated and that the chances of each piece coming up are equally likely.

Solution:
Since each piece is equally likely to appear, each piece has a probability of $ 1/7th $. Furthermore, since the second outcome is independent of the first outcome, the probability will always be $ 1/7th $ for every new piece that appears.
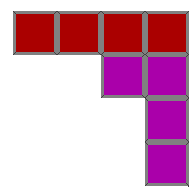
Now, since we have two turns remaining we have to figure out what combinations will allow us to complete the four rows. There are three combinations that allow us complete the rows. They appear as follows:
The pieces of the first solution can be placed in any order (e.g. (1,2) or (2,1)). However, the pieces in the second solution can only be placed in with the purple piece appearing first.
Thus, since we have a probability of $ 1/49th $ $ (1/7 * 1/7) $ chance of obtaining any two piece combination and we have three combinations we could obtain in order to complete the four rows, we have a $ 3*1/49 $ chance of completing the four rows.
$ 3/49 $, or roughly 6.1%, which is not in our favor.