Contents
Homework 9 Solutions, ECE301 Spring 2011 Prof. Boutin
Students should feel free to make comments/corrections or ask questions directly on this page.
Question 1
(a) The given signal has finite duration and hence it is not band-limited.
(b) The given signal has finite duration and hence it is not band-limited.
(c) The given signal has infinite duration and hence it is band-limited.
$ x(t)=\frac{\sin(3\pi t)}{t}=\pi\frac{\sin(3\pi t)}{\pi t} $
$ \begin{align} \mathcal{X}(\omega)&=\pi \cdot \mathfrak{F}\left\{\frac{\sin(3\pi t)}{\pi t}\right\} \\ &=\left\{\begin{array}{ll} \pi , & \mbox{ for } |\omega|<3\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \end{align} $
Thus the Nyquist rate of this signal is $ \omega_s=2(3\pi)=6\pi $.
(d) The given signal has infinite duration and hence it is band-limited.
$ x(t)=\frac{\sin(3\pi(t+5))}{t+5}=\pi\frac{\sin(3\pi(t+5))}{\pi(t+5)} $
$ \begin{align} \mathcal{X}(\omega)&=\pi \cdot \mathfrak{F}\left\{\frac{\sin(3\pi (t+5))}{\pi (t+5)}\right\} \\ &=\left\{\begin{array}{ll} \pi e^{5j\omega} , & \mbox{ for } |\omega|<3\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \end{align} $
Thus the Nyquist rate of this signal is $ \omega_s=2(3\pi)=6\pi $.
Question 2
$ x(t)=e^{j\pi t}\frac{\sin(\pi t)}{t}=\pi e^{j\pi t}\frac{\sin(\pi t)}{\pi t} $
Using frequency shift property of FT, we get:
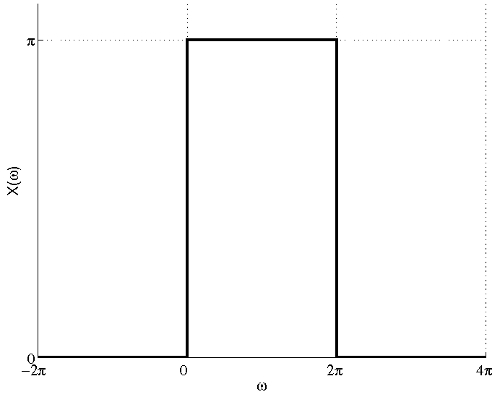
$ \begin{align} \mathcal{X}(\omega)&=\left\{\begin{array}{ll} \pi , & \mbox{ for } |\omega - \pi|<\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \\ &=\left\{\begin{array}{ll} \pi , & \mbox{ for } -\pi <\omega-\pi<\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \\ &=\left\{\begin{array}{ll} \pi , & \mbox{ for } 0<\omega<2\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \end{align} $
The figure below shows the plot of the FT of $ x(t) $.
After sampling with a sampling period T, we get:
$ \mathcal{X_s}(\omega)=\frac{1}{2\pi}\mathcal{X}(\omega)*\mathcal{P}(\omega)=\frac{1}{T}\sum_{k=-\infty}^{\infty}\mathcal{X}(\omega-\frac{2\pi k}{T}) $
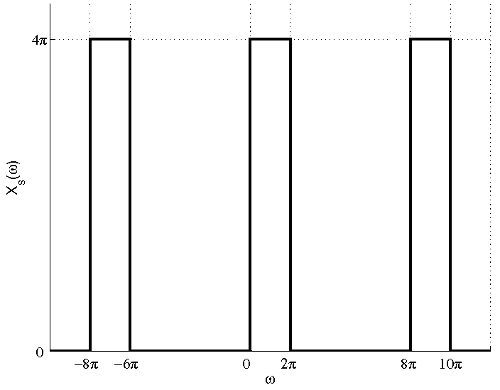
(a) The FT of the signal after sampling with sampling period $ T=\frac{1}{4} $ is shown in the figure below.
From the figure, we can see that there is no aliasing and the signal can be recovered by filtering the sampled signal using the following filter:
$ \mathcal{H}(\omega)=\left\{\begin{array}{ll} \frac{1}{4} , & \mbox{ for } 0<\omega<2\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. $
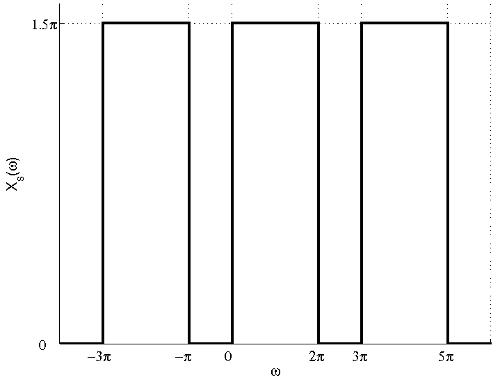
(b) The FT of the signal after sampling with sampling period $ T=\frac{2}{3} $ is shown in the figure below.
From the figure, we can see that there is no aliasing and the signal can be recovered by filtering the sampled signal using the following filter:
$ \mathcal{H}(\omega)=\left\{\begin{array}{ll} \frac{2}{3} , & \mbox{ for } 0<\omega<2\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. $
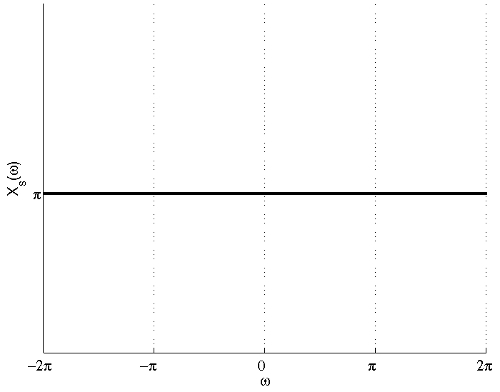
(c) The FT of the signal after sampling with sampling period $ T=2 $ is shown in the figure below.
From the figure, we can see that there is aliasing and thus the signal cannot be recovered.
Question 3
$ \begin{align} \mathfrak{F}\left\{p(t-3)\right\}&=P(\omega)e^{-3j\omega} \\ &=\omega_se^{-3j\omega}\sum_{k=-\infty}^{\infty} \delta(\omega-\omega_s k) \\ &=\omega_s \sum_{k=-\infty}^{\infty} e^{-3j\omega_s k}\delta(\omega-\omega_s k) \text{ Using sampling property of dirac-delta function} \end{align} $
Let $ x_s(t)=x(t)p(t-3) $, then
$ \begin{align} \mathcal{X}_s(\omega)&=\frac{\omega_s}{2\pi} \mathcal{X}(\omega)*\sum_{k=-\infty}^{\infty}e^{-3j\omega_s k}\delta(\omega-\omega_s k) \\ &=\frac{\omega_s}{2\pi} \sum_{k=-\infty}^{\infty}e^{-3j\omega_s k}\mathcal{X}(\omega-\omega_s k) \\ \end{align} $
Note that the exponential term does not depend on $ \omega $, and that at $ k=0 $ it is 1. Thus:
- if $ \omega_s>2\omega_M $, then the signal can be recovered by passing $ x_s(t) $ through the following filter:
- $ \mathcal{H}(\omega)=\left\{\begin{array}{ll} \frac{2\pi}{\omega_s} , & \mbox{ for } |\omega|<\omega_M \\ 0, & \mbox{ elsewhere} \end{array}\right. $
- if $ \omega_s<2\omega_M $, then there will be aliasing and the signal cannot be recovered.
Question 4
Since $ x(t) $ is sampled with a sampling period $ T_s=\pi/\omega_0 $, then the sampling rate is $ \omega_s=2\omega_0 $ and hence there is no aliasing.
Taking the FT of both sides of the system equation we get:
$ \mathcal{Y}(\omega)=j\omega\mathcal{X}(\omega) $
and hence the frequency response of the CT system is:
$ \mathcal{H}(\omega)=j\omega $
Using the relationship between the frequency response of the CT system and the DT system, we get:
$ \begin{align} \mathcal{H}_d(\omega)&=\mathcal{H}(\frac{\omega}{T_s}) \text{ for }|\omega|<\pi \\ &=j\frac{\omega}{T_s} \text{ for }|\omega|<\pi \end{align} $
Now in order to get the impulse response of the DT system we take the IDTFT of the frequency response above:
$ \begin{align} h_d[n]&=\frac{1}{2\pi}\int_{-\pi}^{\pi}j\frac{\omega}{T_s} e^{j\omega n} d\omega\\ &=\frac{j}{2\pi T_s} \int_{-\pi}^{\pi} \omega e^{j\omega n}d\omega \\ &=\frac{j}{2\pi T_s} \left[\omega \frac{e^{j\omega n}}{jn}\right]^{\pi}_{-\pi} + \frac{j}{2\pi T_s}\left[\frac{e^{j\omega n}}{n^2}\right]_{-\pi}^{\pi} \\ &=\frac{1}{2T_s n} [e^{j\omega \pi}+e^{-j\omega \pi}] + \frac{j}{2\pi T_s n^2}[e^{j \pi n} - e^{-j \pi n}] \\ &=\frac{(-1)^n}{T_s n} \\ &=\frac{\omega_0 (-1)^n}{\pi n} \end{align} $
Note that an impulse response is sufficient to characterize an LTI system.