Discrete-time Fourier transform of a window function
Used in ECE438.
Consider the perfect discrete-time window function
$ w[n]= \left\{ \begin{array}{ll} 1,&\text{ if }0 \leq n < N \\ 0, & \text{ else}. \end{array} \right. $
The DTFT of that window function is
$ W(\omega) =\frac{e^{\frac{-j \omega (N-1)}{2}} \sin\left( \frac{\omega N}{2}\right)}{\sin \left( \frac{\omega}{2} \right)} $.
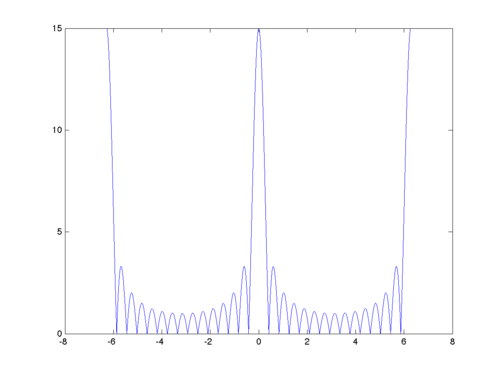
Below is the graph of the magniture of $ W(\omega) $ for $ N=15 $.
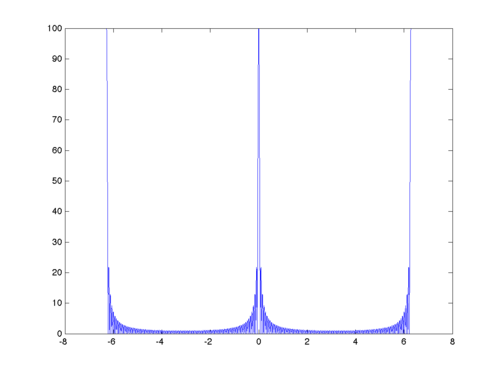
Below is the graph of the magniture of $ W(\omega) $ for $ N=100 $. Observe that the ripples are "thinner" and more numerous than in the previous case of $ N=10 $.
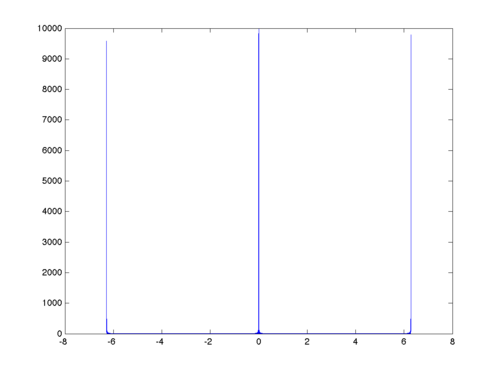
Below is the graph of the magniture of $ W(\omega) $ for $ N=10000 $.
Observe the close resemblance of this graph to that of the magnitude of the Fourier transform of the corresponding continuous-time window.