Rep Function:
A rep function periodically repeats another function with some specified period T ( basically sampling time). Mathematically a rep operator is a function x(t) convoluted with a summation of shifted deltas:
$ rep_T [x(t)] = x(t)* \mathrm {P_T}(t) = x(t)* \sum_{k=-\infty}^{\infty}\delta(t-kT) $
$ {{=}}\sum_{\infty}^{\infty}x(\delta(t-kT) $ $ {{=}}\sum_{k=-\infty}^{\infty}x(t-kT) $
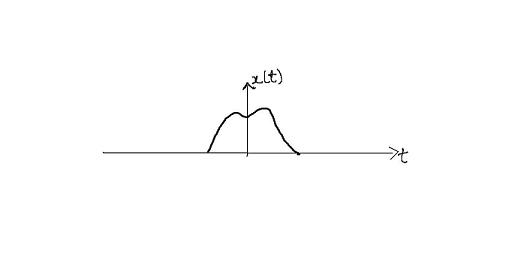
If below is the x(t):
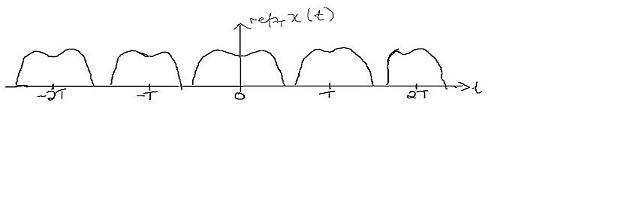
Then the $ rep_T [x(t)] $ looks like:
The resulting function is periodic with period T. To keep x(t) repeating without aliasing, the minimum sampling period should be $ \geqq 2 * T $
Comb Function
A comb function multiplies a function with a periodic train of impulses.
$ comb_T[x(t)] = x(t) . \sum_{k=-\infty}^{\infty}\delta(t-kT) = x(t) . \mathrm{P_T} (t) $
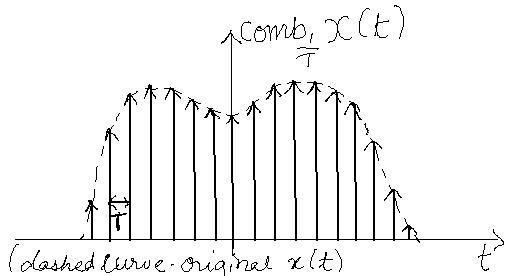
Using the same x(t) as above as our function to be multiplied with a train of impulses, we get:
Note: The Fourier Transform of a $ rep_T $ x(t) gives the comb function of x(t) but in the frequency domain.
$ \mathfrak{F} (rep_T [x(t)]) = \mathfrak{F} ( x(t) * P_T (t) ) = \mathrm{X}(f).\mathrm{P_T}(f) $
Where
$ \mathrm{P_T}(f) = \mathfrak{F} ( \sum_{k} \delta(t-kT)) $
$ {{=}} \mathfrak{F} (\sum_{n=-\infty}^{\infty} \frac{1}{T} exp \frac{j2nt\pi}{T} ) $ $ {{=}} \sum_{n=-\infty}^{\infty} \frac{1}{T} \delta( f - \frac{n}{T} ) $ $ {{=}} \frac{1}{T} P_T (f) $
Therefore:
$ \mathrm{X}(f).\frac{1}{T}P_T (f) {{=}} \frac{1}{T}comb_\frac{1}{T} [ \mathrm{X}(f)] $
To conclude the transform relationship between the comb operator and rep operator surfaces when we take the operator's Continuous Time Fourier Transform :
$ comb_T [x(t)] \iff \frac{1}{T}rep_\frac{1}{T} [ \mathrm{X}(f)] $
$ rep_T [x(t)] \iff \frac{1}{T}comb_\frac{1}{T} [ \mathrm{X}(f)] $