Lecture 15 - Parzen Window Method OldKiwi - Rhea

ECE662 Main Page

Class Lecture Notes

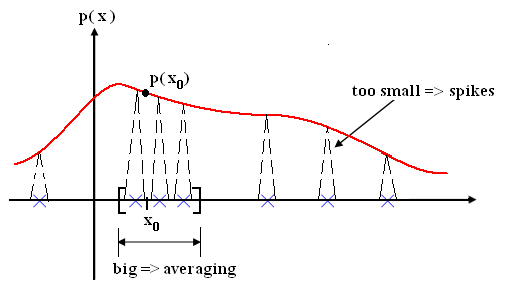
Figure 1

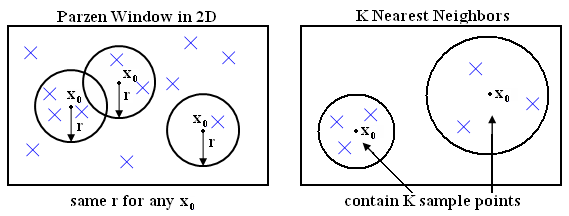
Figure 2

Parzen Window Method

- Step 1:** Choose "shape" of your window by introducing a "window function"

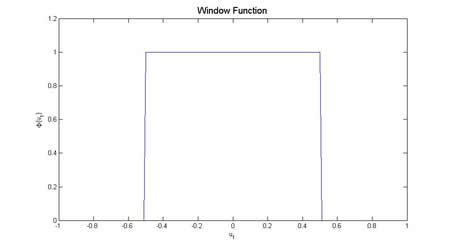
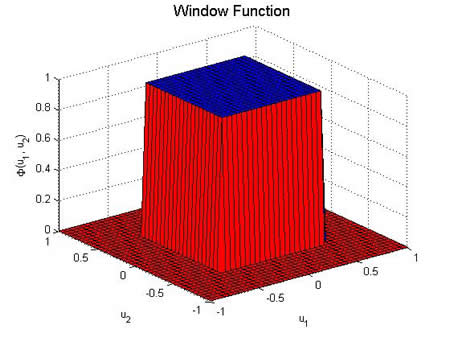
e.g. if $$ R_i $$ is hybercube in $\mathbb{R}^n$ with side-length $$ h_i $$ , then the window function is $\varphi$ .

$\varphi(\vec{u})=\varphi(u_1, u_2, \ldots, u_n)=1$ if $|u_i|<\frac{1}{2}, \forall i$ otherwise 0.

Examples of Parzen windows

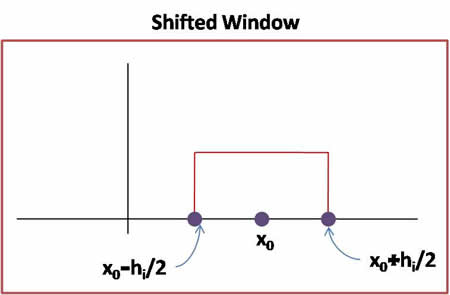
Given the shape for parzen window by $\varphi$ , we can scale and shift it as required by the method.

$\varphi(\frac{\vec{x}-\vec{x_0}}{h_i})$ is window centered at $\vec{x_0}$ scaled by a factor $$ h_i $$ , i.e. its side-length is $$ h_i $$ .

- Step 2:** Write the density estimate of $p(\vec{x})$ at $\vec{x_0} \in R_i$ using window function, denoted by $p_i(\vec{x_0})$ .

We have number of samples for $\{\vec{x_1}, \vec{x_2}, \ldots, \vec{x_i}\}$ inside $$ R_i $$ denoted by $$ K_i $$

$\sum_{l=1}^{i}\varphi(\frac{\vec{x_l}-\vec{x_0}}{h_i})$

So, $p_i(\vec{x_0})=\frac{k_i}{iV_i}=\frac{1}{iV_i}\sum_{l=1}^{i}\varphi(\frac{\vec{x_l}-\vec{x_0}}{h_i})$

Let $\delta_i(\vec{u})=\frac{1}{V_i}\varphi(\frac{\vec{u}}{h_i})$

$p_i(\vec{x_0})=\frac{1}{i}\sum_{l=1}^{i}\delta_i(\vec{x_l}-\vec{x_0})$

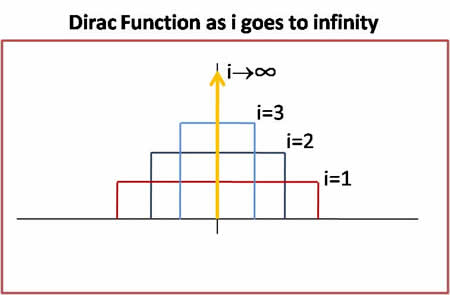
This last equation is an average over impulses. For any l, $\lim_{h_i->0}\delta(\vec{x_l}-\vec{x_0})$ is [Dirac delta Function]. We do not want to average over dirac delta functions. Our objective is that $p_i(\vec{x_0})$ should converge to true value $p(\vec{x})$ , as $i\rightarrow \infty$

.. |MSS1| image:: tex

alt: tex: \lim_{i\rightarrow \infty}E\{p_i(\vec{x_0})\}=p(\vec{x_0})

.. |MSS2| image:: tex

alt: tex: \lim_{i\rightarrow \infty}Var\{p_i(\vec{x_0})\}=0

.. |MSS3| image:: tex

alt: tex: p_i(\vec{x_0}) \longrightarrow p(\vec{x_0})

- What does convergence mean here?**

Observe $\{p_i(\vec{x_0})\}$ is a sequence of random variables since $p_i(\vec{x_0})$ depends on random variables |sample_space_i|. What do we mean by convergence of a sequence of random variables (There are many definitions). We pick "Convergence in mean square" sense, i.e.

If |MSS1|

and |MSS2|

then we say |MSS3| in mean square as |i_tends_infty|

.. |kkh01| image:: tex

alt: tex: E(p_i(\vec{x_o}))

.. |kkh02| image:: tex

alt: tex: p(\vec{x_o})

.. |kkh03| image:: tex

alt: tex: i\to\infty

.. |kkh04| image:: tex

alt: tex: h_i \to\infty

.. |kkh05| image:: tex

alt: tex: V_i\to\infty

.. |kkh06| image:: tex ..alt: tex: Var(p_i\vec{x_o})

- First condition:**

From the previous result, |jinha_pix0|

.. |jinha_pix0| image:: tex

alt: tex: \displaystyle p_i (x_0) = \frac{1}{i} \sum_{l=1}^{i} \delta_i (\vec{x}_l - \vec{x}_0)

|jinha_epix0|

.. |jinha_epix0| image:: tex

alt: tex: \displaystyle E[p_i(x_0)] = \frac{1}{i} \sum_{l=1}^{i} E[ \delta_i (\vec{x}_l - \vec{x}_0) ] = \frac{1}{i} \sum_{l=1}^{i} \int \delta_i (\vec{x}_l - \vec{x}_0) p(\vec{x}_l) dx_l \rightarrow p(\vec{x}_0)

We don't need an infinity number of samples to make |kkh01| converge to |kkh02| as |kkh03|.

We just need |kkh04| (iie. |kkh05|)

- To make it sure** |jinha_varpix0|, what should we do?

.. |jinha_varpix0| image:: tex

alt: tex: Var(p_i(x_0)) \rightarrow 0

|jinha_varpix0_1|

.. |jinha_varpix0_1| image:: tex

alt: tex: \displaystyle Var(p_i(x_0)) = Var(\sum_{l=1}^{i} \frac{1}{i} \delta_i(\vec{x}_l - \vec{x}_0)) = \sum_{l=1}^{i} Var(\frac{1}{i} \delta_i(\vec{x}_l - \vec{x}_0))

|jinha_varpix0_2|

.. |jinha_varpix0_2| image:: tex

alt: tex: \displaystyle = \sum_{l=1}^{i} E \left[ \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} - E\left[ \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right] \right)^2 \right] = \sum_{l=1}^{i} E \left[ \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right)^2 \right] - \left( E\left[ \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right] \right)^2

We know that second term is non-negative, therefore we can write

|jinha_varpix0_3|

.. |jinha_varpix0_3| image:: tex

alt: tex: \displaystyle Var(p_i(x_0)) \le \sum_{l=1}^{i} E \left[ \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right)^2 \right]

|jinha_varpix0_4|

.. |jinha_varpix0_4| image:: tex

alt: tex: \displaystyle \rightarrow Var(p_i(x_0)) \le \sum_{l=1}^{i} \int \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i} \right)^2 p(x_l) dx_l

|jinha_varpix0_5|

.. |jinha_varpix0_5| image:: tex

alt: tex: \displaystyle \rightarrow Var(p_i(x_0)) \le \sum_{l=1}^{i} \frac{1}{i^2} \int \frac{\psi \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i}\right)}{V_i} \frac{\psi \left( \frac{\delta_i(\vec{x}_l - \vec{x}_0)}{i}\right)}{V_i} p(x_l) dx_l

|jinha_varpix0_6|

.. |jinha_varpix0_6| image:: tex

alt: tex: \displaystyle \rightarrow Var(p_i(x_0)) \le \frac{1}{i V_i} sup\psi \int \sum_{l=1}^{i} \delta_i (x_l - x_0) p(x_l) dx_l

|jinha_varpix0_7|

.. |jinha_varpix0_7| image:: tex

alt: tex: \displaystyle \therefore Var(p_i(x_0)) \le \frac{1}{i V_i} sup\psi E [p_i(x_0)]

If fixed i=d, then as |a_1| increased, |a_2| decreased.

But, if |a_3| , as |a_4|

(for example, if |a_5|)

then, |a_6|

.. |a_1| image:: tex

alt: tex: v_i