Definition of Linear System
A system is considered linear if for any constants a, b that exist within the complex domain and for any inputs $ x_1(t)\! $ and $ x_{2}(t)\! $ yielding outputs $ y_{1}(t)\! $ and $ y_2(t)\! $ respectively, the response to $ x_1(t) + bx_{2}(t)\! $ is $ y_1(t) + by_{2}(t)\! $
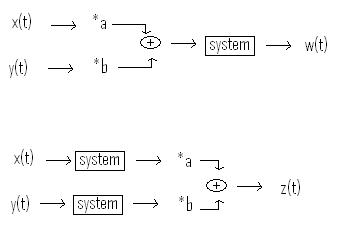
This is saying that if i have 2 inputs of x(t) and y(t) and put them through a system, then multiply the 2 outputs by a constant, and add them together to get my final signal i should get the same if i multiply the two input signals by the constant first and add them, then send them through the system.
In the case above, for the systems to be linear, z(t) must equal w(t)
Examples
Linear System
Equation: $ y(t) = x(t)/2 $
$ x_{1}(t) \to (system) \to *a \to $ $ + \to a x_{1}(t)/2 + b x_{2}(t)/2 $ $ x_{2}(t) \to (system) \to *b \to $
$ x_{1}(t) \to *a \to $ $ + \to (system) \to (a x_{1}(t) + b x_{2}(t))/2 = a x_{1}(t)/2 + b x_{2}(t)/2 $ $ x_{2}(t) \to *b \to $
Non Linear System
Equation: $ y(t) = e^{x(t)} $
$ x_{1}(t) \to (system) \to *a \to $ $ + \to a e^{x_{1}(t)} + b e^{x_{2}(t)} $ $ x_{2}(t) \to (system) \to *b \to $
$ x_{1}(t) \to *a \to $ $ + \to (system) \to e^{a x_{1}(t) + b x_{2}(t)} $ $ x_{2}(t) \to *b \to $