Part 1
The function was chosen at random from HW1: HW1.4 Hang Zhang - Periodic vs Non-period Functions_ECE301Fall2008mboutin
$ \,x(t)=2cos(2\pi t)\, $
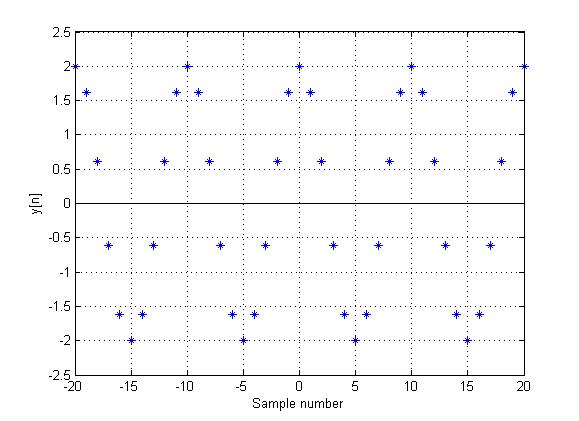
Periodic Signal in DT:
If $ x(t) $ is sampled at $ period=0.1 $, the function
$ \,y[n]=x[0.1n]=2cos(\frac{2\pi n}{10})\, $
is periodic, since
$ \,\exists N\in \mathbb{Z}, N\not= 0\, $ such that $ \,y[n]=y[n+N], \forall n\in \mathbb{Z}\, $
$ \,2cos(\frac{2\pi n}{10})=2cos(\frac{2\pi n}{10}+\frac{2\pi N}{10})\, $
This is true when
$ \,\frac{2\pi N}{10}=2\pi \, $
$ \,N=10\, $
This can be seen in the following plot:
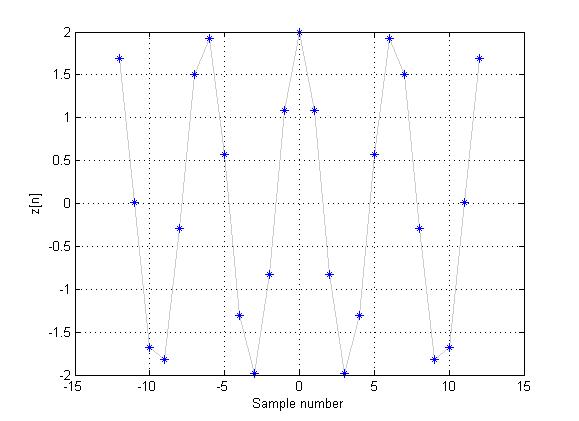
Non-Periodic Signal in DT:
However, if $ x(t) $ is sampled at $ period=1/2\pi $, the function
$ \,z[n]=x[\frac{n}{2\pi}]=2cos(n)\, $
is not periodic in DT, since there is no integer $ N\in \mathbb{Z}, N\not= 0 $ such that
$ \,z[n]=z[n+N], \forall n\in \mathbb{Z}\, $
$ \,2cos(n)=2cos(n+N)\, $
This would be true when
$ \,N=2\pi k, k\in \mathbb{Z}, k\not= 0\, $
$ \,\frac{N}{k}=2\pi \, $
but, $ 2\pi $ is irrational, thus there are no values for the integers $ \,N,k\, $ that will satisfy this equation.
This can be seen in the following plot:
Part 2
TODO: Having problems performing this on arbitrary functions, such as $ \,x(t)=e^{t}\, $, since the infinite sum will result with an undefined function.