Communication and Reducibility
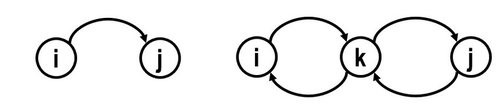
Before moving on and discovering more behaviors of Markov chains, we need to classify the properties of states first. In the previous section, we use $ P_{ij} $ to represent the transition probability of state changing from $ i $ to $ j $; now, we use $ P_{ij}^{n} $ to denote the transition probability of state changing from $ i $ to $ j $ after $ n $ step. If $ P_{ij}^{n} \geq 0 $ for all $ n \geq 1 $, we say state $ j $ is accessible from state $ i $, which also can be written as $ i \rightarrow j $. If $ i \rightarrow j $ and at the same time $ j \rightarrow i $, then we say that state $ i $ and state $ j $ communicate, which can be denoted as $ i \leftrightarrow j $. On the other hand, if $ P_{ij}^{n} = 0 $ or $ P_{ji}^{n} = 0 $, or if both of them come into existence, we claim that state $ i $ and state $ j $ do not communicate. The diagrams below illustrate these two cases.