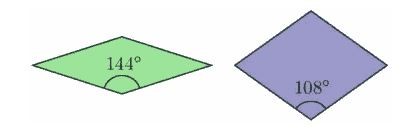
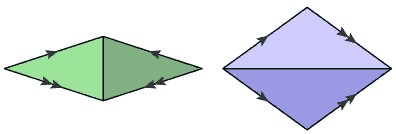
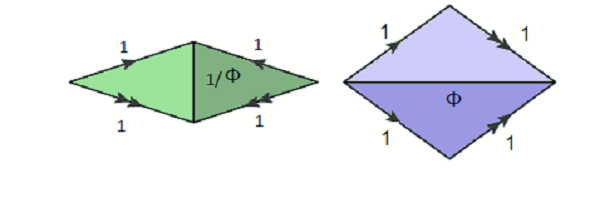
Naturally, Penrose tilings cannot be found too easily in nature; it is why Penrose did not discover and create them until the 1970’s. On the contrary, Penrose tilings are very deliberately contrived structures, ones that may require concrete steps to follow. Before we begin describing how they are constructed, let us first consider the two rhombs in question in the tilings. A picture of the two rhombs is shown below.
One of the utmost important things about these two rhombi is their very intrinsic connection to the golden ratio, Φ, (sqrt(5)+1)/2. This number appears in many contexts and will be an integral part of Penrose tilings with these two shapes. First, let us look at these two shapes in terms of the image below.
The pentagon, as seen in Penrose’s first tiling, is important first and foremost because of its five-fold symmetry, which will occur at most once in a Penrose tiling using rhombs. It is also connected to tilings with rhombs because the rhombs are actually formed by the pentagon. We will see the rhombs formed in the image below.
Note that the two rhombs, which we can take to be the very rhombs we wish to concern ourselves in this discussion, each have different diagonal values. The ratio of the thick rhomb’s longer diagonal to the side length will always be the golden ratio, Φ, while the ratio of the thin rhomb’s short diagonal to the side length will always be 1/Φ. By rearranging the pieces of the pentagon shown in the first part of this discussion, we can create the rhombs which will be used in Penrose tilings, and these ratios will always hold true. Φ will show up several more times in our discussion. In order to showcase these other relationships, let us discuss how Penrose tilings can be generated.
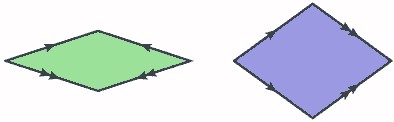
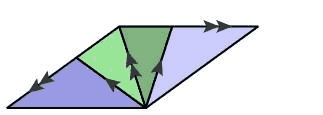
There are some matching rules that should be taken care of while generating Penrose Tilings. This means that certain things must be considered when “matching” rhombs to adjacent ones. Commonly, one may place arrows such that both the directions and numbers of these arrows would match in adjacent rhombus edges. This can be done somewhat arbitrarily like so.
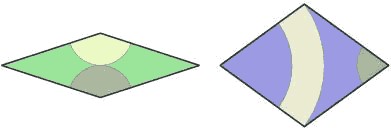
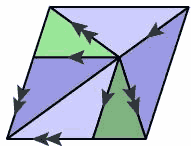
Another matching approach would be to decorate the rhombs in such a way that two adjacent rhombs always fit together consistently. Notice in the tiling below how the white portion of the right rhombus always connects to either another white portion or the light green portion of the left one.
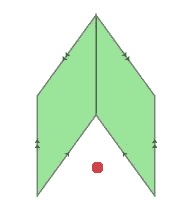
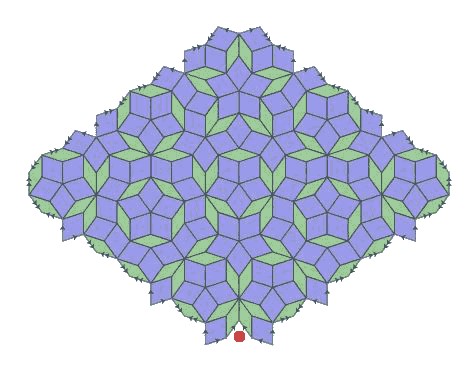
A naive approach to generate a tiling would be to lay down some “rhombs” in a random fashion and see if there is any way to keep continuing the tiling. This might lead us to the point where there remain spaces that cannot be tiled using the rhombs based on the matching rules. For example, in the figure below, none of the rhombs could satisfy the space at the red dot.
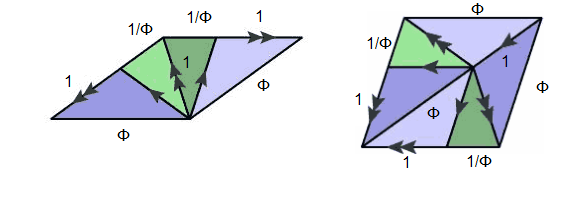
It is not possible to create consistent tilings only using the matching rules. Some other assumptions or rules have to be used in order to end up with better tilings. One such method is called the Method of Inflation, where each rhomb is broken into half as follows.
The possibilities for adjacent half-rhombs, then, become extremely stringent, considering there are only two options for each side of the half-rhomb. We find that these half-rhombs can be combined in two different ways, as shown below.
Astoundingly, we find that these new “patches” of previous half-rhombs are actually the exact same rhombs as before; they have just been scaled upwards by a factor of Φ.
When we take the half-rhombs of our previous rhombs, we find that we split the thin rhomb by the short diagonal and the thick rhomb by the long one. This means that the length of the “bottom” of the triangles formed by the thin rhomb are both 1/Φ, while the bottoms for the triangles formed by the thick rhomb are each Φ.
For both rhombs, the side length should be the same, while the diagonal relationships should still hold true. Let us now test if this is the case.
For the left new rhomb, the base has length Φ, as it is the line we split the previous thick one in half by. This is likewise for the right side of that rhomb. The top and left, then, are each 1 + 1/Φ, which, remarkably, is Φ. The short diagonal is 1, as it is just the side length we had chosen for the previous thin rhomb. This makes sense, as it should be the side length divided by Φ.
For the right one, one can imagine flipping the left rhomb by 180 degrees and going through the same order of calculations as the left. The side lengths will come out the same, and the long diagonal turns out to be 1 + Φ, which, by definition, is just Φ squared. Thus for the thick rhomb, the long diagonal is Φ times the side length, just as it was in the previous rhombs.
Though we chose a side length of 1 for our initial rhombs, any side length can be chosen and the relationship will be the same. After this method, the side length will be scaled upward by Φ, and the short diagonal of the thin rhomb will be the new side length divided by Φ, while the long diagonal of the thick rhomb will be the new side length multiplied by Φ.
After this scaling has occurred, the newly generated rhombs can be used to generate a new Penrose tiling obeying the matching rules, which might look like the image below. Notice that the new rhombs have been denoted by thicker black outlines.
Remarkably, this tiling is now just a combination of thick and thin rhombs, just as before. If one so chooses, one can easily use the Method of Inflation once again on these rhombs, then again on the rhombs that form a tiling after doing so. By continuously scaling new rhombs by the golden ratio, one can create a seemingly endless number of potential Penrose tilings. In fact, continuously doing this for our original choices of rhombs leads to Penrose’s original tiling, as shown below.
The thickening lines in this image represent greater and greater inflations using the method. These inflations, of course, will become infinitely large, as their tiles become scaled by Φ.
We have now seen techniques and methods for developing Penrose tilings, including connections to the golden ratio in terms of developing the tiles used and creating a seemingly infinite number of potential tilings based on just two simple shapes. There is, however, one last connection related to the golden ratio that is certainly worth mentioning. When the number of tiles and the tiling itself becomes infinitely large, the ratio of thick to thin rhombs in the tiling approaches Φ, the golden ratio. Not only does the golden ratio dictate where the tilings come from and how many different tilings one can create, but this last fact about the golden ratio seals just how important this one number is in dealing with Penrose tilings. Even if one has complete control over placement and creation of tilings, as that person continues, they will be bounded by this limit.