Introduction

The Fibonacci sequence is one of the more widely known integer sequences used in mathematics. An integer sequence is simply an ordered list of integers (0, ±1, ±2, …). The Fibonacci sequence is typically constructed recursively; the nth term of the sequence can be determined by the previous terms. Beginning with 0 and 1, the Fibonacci sequence is given by:

The value of the golden ratio can be found using a variety of method. For example, consider the golden rectangle seen below.

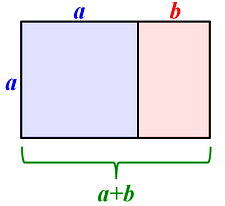
A golden rectangle is constructed by taking a square of side length a, and extending it a length b so that the following is true:

The golden ratio is the value $ \frac{a}{b} $ that solves this equation. If we substitute $ x = \frac{a}{b} $, we can see that only a simple quadratic equation must be solved:

Which has solutions:

The first solution (which is positive) is defined as the golden ratio. The golden ratio is strongly related to the Fibonacci sequence, as the ratio between consecutive terms of the Fibonacci sequence approaches . Consider the ratio between F_n and F_n-1, and between F_n-1 and F_n-2. Since the sequence approaches a fixed ratio, as $ n \rightarrow \infty $, we have:

Using the recursive relationship that defines the Fibonacci series, we can rewrite the above equation as:

Substituting $ x = \frac{F_{n-1}}{F_{n-2}} $, we obtain the same equation as for the golden rectangle:

In fact, the golden ratio can be used to provide an explicit equation for the n^th Fibonacci number:

Back to Home