MICROELECTRONICS and NANOTECHNOLOGY (MN)
Question 3: Field Effect Devices
August 2013
Questions
All questions are in this link
Solutions of all questions
1)$ \begin{align*} Q&=C_{ox}(V_{gs}-V_t)\\ &=\frac{\epsilon_0\epsilon_r}{t_{ox}}\times0.5\\ &=8.9\times10^{-7}C/cm^2 \text{ (chk)} \end{align*} $
------------------------------------------------------------------------------------
2) $ I_d = \mu_nC_{ox}\frac{W}{L}(V_{GS-V_t}V_{ds}) $
$ \begin{align*} \implies R_d=\frac{V_{ds}}{I_d}&=\frac{1}{500\times\frac{\epsilon_0\epsilon_r}{t_{ox}}\times\frac{0.5\mu}{200n}\times0.5}\\ &=\frac{8}{8.9}\times10^3\Omega\\ &=0.89k\Omega \text {(chk)} \end{align*} $
------------------------------------------------------------------------------------
3) $ \begin{align*} I_{d1}&=\frac{V_{ds}}{R_d}=\frac{10mV}{0.89k\Omega}=11.23\mu A\\ I_{d2}&=\frac{V_{ds}}{R_d+R_s+R_d'}=\frac{10mV}{2.89k\Omega}=3.4\mu A\\ \triangle I_{D2}&=7.7\mu A \end{align*} $
------------------------------------------------------------------------------------
4) For ideal MOSFET; $ g_d=0 $ in saturation $ \begin{align*} \end{align*} $
------------------------------------------------------------------------------------
5) $ \begin{align*} V_{SF}&=\frac{C_{ox}}{C_{ox}+(C_{it}+C_{dep})}\cdot V_{gs}\\ &=C1\cdot v_{gs} \end{align*} $
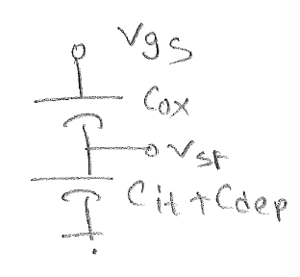
------------------------------------------------------------------------------------
6)$ \begin{align*} \ln I_d&=\ln A+\frac{qV_{SF}}{kT}\\ &=\ln A+ \frac{qC_1V_{gs}}{kT} \end{align*} $
$ \frac{d(\ln I_d)}{dv_{gs}}=\frac{qC_1}{kT} $
$ \begin{align*} S&=\ln 10\cdot\frac{kT}{qC_1}\\ &=\ln 10\cdot\frac{kT(C_{ox}+C_{it}+C_{dep})}{qC_{ox}}.....1\\ &=\ln 10\cdot\frac{kT}{q}\cdot\frac{v_{gs}}{V_{SF}} \end{align*} $
------------------------------------------------------------------------------------
7) Eqn 1.
------------------------------------------------------------------------------------
8)$ \begin{align*} \frac{S}{S_{ideal}}&=\frac{C_{ox}+C_{it}}{C_{ox}}; C_{dep}=0\\ C_{ox}&=\frac{\epsilon_0\cdot\epsilon_r}{t_{ox}}\times WL\\ &=1.78\times10^{-15}F \end{align*} $ $ \therefore\frac{S}{S_{ideal}}=1.112 $
------------------------------------------------------------------------------------
9)$ \begin{align*} L'&=L=2r;\bigg(\sqrt{1+\frac{2w_T}{r;}}-1\bigg)\\ &=L-\triangle L \end{align*} $ affected by c, f, h
------------------------------------------------------------------------------------
10) Need $ \triangle L\downarrow$\\ So; <math> <math>r_J\downarrow c $
$ w_T\downarrow f $ $ \downarrow h $ </math> ------------------------------------------------------------------------------------

