Question

Solution

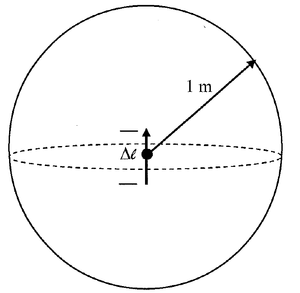
$ \begin{equation*} \left.\begin{aligned} \nabla\cdot \bar{B}&=0\\ \oint_S \bar{B}\cdot d\bar{S}&=0 \end{aligned}\right\} \longrightarrow \Phi=\oint_S \bar{B}\cdot d\bar{S} \Longrightarrow \boxed{ \Phi=\oint_S \bar{B}\cdot d\bar{S}=0} \end{equation*} $

The magnetic flux through this closed surface is $ \Phi $

$ \begin{equation*} \boxed{\Phi=0} \end{equation*} $

Question

Solution

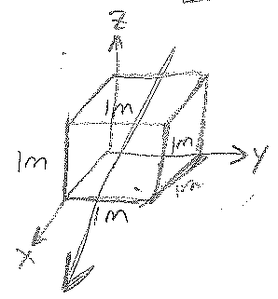
$ \begin{align*} \nabla\dot \bar{D} &= \rho \\ \quad (\frac{\partial}{\partial x}\hat{x}+\frac{\partial}{\partial y}\hat{y}+\frac{\partial}{\partial z}\hat{z})\cdot(2\hat{x})&=\rho \\ \frac{\partial}{\partial x}(2)&=0=\rho \quad \text{(no charge)} \end{align*} $

$ \underline{Also}: \begin{align*} \oint \bar{D}\cdot d\bar{S}&=Q\\ &=\int2(dS_x)+\int2(-dS_x)=2-2=\boxed{0} \end{align*} $

Question

Part 1.

Consider $ n $ independent flips of a coin having probability $ p $ of landing on heads. Say that a changeover occurs whenever an outcome differs from the one preceding it. For instance, if $ n=5 $ and the sequence $ HHTHT $ is observed, then there are 3 changeovers. Find the expected number of changeovers for $ n $ flips. Hint: Express the number of changeovers as a sum of Bernoulli random variables.

Click here to view student answers and discussions

Part 2.

Let $ X_1,X_2,... $ be a sequence of jointly Gaussian random variables with covariance

$ Cov(X_i,X_j) = \left\{ \begin{array}{ll} {\sigma}^2, & i=j\\ \rho{\sigma}^2, & |i-j|=1\\ 0, & otherwise \end{array} \right. $

Suppose we take 2 consecutive samples from this sequence to form a vector $ X $, which is then linearly transformed to form a 2-dimensional random vector $ Y=AX $. Find a matrix $ A $ so that the components of $ Y $ are independent random variables You must justify your answer.

Click here to view student answers and discussions

Part 3.

Let $ X $ be an exponential random variable with parameter $ \lambda $, so that $ f_X(x)=\lambda{exp}(-\lambda{x})u(x) $. Find the variance of $ X $. You must show all of your work.

Click here to view student answers and discussions

Part 4.

Consider a sequence of independent random variables $ X_1,X_2,... $, where $ X_n $ has pdf

$ \begin{align}f_n(x)=&(1-\frac{1}{n})\frac{1}{\sqrt{2\pi}\sigma}exp[-\frac{1}{2\sigma^2}(x-\frac{n-1}{n}\sigma)^2]\\ &+\frac{1}{n}\sigma exp(-\sigma x)u(x)\end{align} $.

Does this sequence converge in the mean-square sense? Hint: Use the Cauchy criterion for mean-square convergence, which states that a sequence of random variables $ X_1,X_2,... $ converges in mean-square if and only if $ E[|X_n-X_{n+m}|] \to 0 $ as $ n \to \infty $, for every $ m>0 $.

Click here to view student answers and discussions

Back to ECE Qualifying Exams (QE) page