Contents
ECE Ph.D. Qualifying Exam in Communication Networks Signal and Image processing (CS)
Question 5, August 2013, Part 1
Solution:
a) $ \gamma=1 $
b)
$ (x_r,y_r)=(\frac{a}{a+d+g},\frac{d}{a+d+g}) $
$ (x_g,y_g)=(\frac{b}{b+e+h},\frac{e}{b+e+h}) $
$ (x_b,y_b)=(\frac{c}{c+f+i},\frac{f}{c+f+i}) $
c)
$ (x_w,y_w)=(\frac{a+b+c}{a+b+c+d+e+f+g+h+i},\frac{d+e+f}{a+b+c+d+e+f+g+h+i}) $
d)
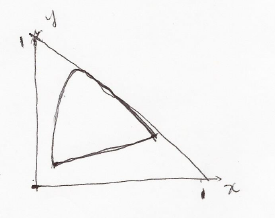
If $ (X,Y,Z)=(0,1/2,1/2) $, then $ (x,y)=(0,1/2) $.
In the chromaticity diagram, this point is outside the horse shoe shape, so its RGB values are not all larger than 0 ($ R<0,G>0,B>0 $).
e) We are likely to see quantization artifact in dark region.
Solution 2:
a) The gamma is 1
b)
$ (x_r,y_r)=(\frac{a}{a+d+g},\frac{d}{a+d+g}) $
$ (x_g,y_g)=(\frac{b}{b+e+h},\frac{e}{b+e+h}) $
$ (x_b,y_b)=(\frac{c}{c+f+i},\frac{f}{c+f+i}) $
c)
$ (x_w,y_w)=(\frac{a+b+c}{a+b+c+d+e+f+g+h+i},\frac{d+e+f}{a+b+c+d+e+f+g+h+i}) $
d) This color is imaginary. At least one of R,G,B values must be negative. Cannot be produced by this device.
The student can be more specific about the positive or negative of each R,G,B value of this color.
e) Quantization artifacts in the dark area.
Related Problem
Consider a color imaging device that takes input values of $ (r,g,b) $ and produces ouput $ (X,Y,Z) $ values given by
$ \left[ {\begin{array}{*{20}{c}} X\\ Y\\ Z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} a&b&c\\ d&e&f\\ g&h&i \end{array}} \right]\left[ {\begin{array}{*{20}{c}} r^\alpha\\ g^\alpha\\ b^\alpha \end{array}} \right] $
a) Calculate the white point of the device in chromaticity coordinates.
b) What are the primaries associated with the r,g, and b components respectively?
c) What is the gamma of the device?
d) Draw the region on the chromaticity diagram corresponding to $ r < 0, g > 0, b > 0 $.