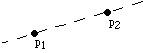Alison Brown (brown398@purdue.edu)

Pinar Temiz (ptemiz@purdue.edu)

Origami Groups

aharoni

Introduction/History of Origami

Origami, despite what many math believe, is orignally thought to have begun in China (PBS, 2009). This art form was brought to Japan from China. Coming from the Japanese words oru(to fold) and kami(paper)origami was only at first only available for the weathly since paper was so expensive. Since the expense was so great, oragami was mainly used for ceremonies and religious events. However, as time passed and paper was produced on a larger scale, origami became available for both the rich and poor. For the same reason, people starting creating origami for art instead of for ceremonial/religous purposes. For a long time this art form was simply passed down from one generation to the next without writing. In fact the first written instructions were by Akisato Rito called "Thousand Crane Folding". Older forms of origami were simply paper folder to make a design such as a crane. However, modern origami is created by artists. Modern designs can even look like puzzles created by mathematicians. Akira Yoshizawa is considered one of the fathers of modern origami because he created a system of folding patterns, symbols, arrows, and diagrams to streamline this art. Now, more and more people are creating this art using mathematical principles and ideas. A few of the "mathematical origami pioneers" include Jun Maekawa, Peter Engel, Robert Lang, and Erik Demaine. All of the mathematicians use particular constructs in order to create the amazing origami structures seen today.

What are Origami Groups?

    -Development of the math

-Related Mathematicians and Real Life Examples:

A related Mathemetician who’s work is really interesting is Robert J. Lang. He has a very good way of explaining how origami works and how we use origami in everyday life even in ways we would not have even thought. For example, he came up with an idea to get a telescope with a lens with a diameter of 100 meters, which would be the size of a football field, into space to orbit around the Earth 22,000 miles away. Robert Lang knew that the bigger the telescope was, the better and sharper the images would be and hence he tried to make it as big as it could be with still being able to take it up into space and the idea was the it would be a thin as a sheet of paper. All space vehicles such as heavy lift rockets usually had a capacity to carry objects of a 4 meter diameter and that is 10 meters long. This meant that the lens had to be folded, crumpled or stuffed into the tube of the rocket. However if there was an undesired fold then this would ruin the optical performance of the lens, therefore it had to have to be collapsed into a smaller shape by a controlled set of creases whose locations and structure would not degrade the optical performance. In the 1980’s origami had been used in space also for a solar panel designed by Koryo Miura to fly in a Japanese satellite. There were different structures and ideas being adapted for the Eyeglass telescope using origami and applying it to the telescope. They needed a radically symmetric structure and collapsed on a finite number of creases that fit within a cylindrical form factor such as a rocket. The origami structure that was settled with was called the ‘Umbrella’ as it resembled a collapsible umbrella which folded from a large flat disk down to a much smaller bordered cylinder.

How it works

(O1) Given two points p1 and p2 we can fold a line connecting them.

Relation to other fields of mathematics

Origami relates in many ways to different fields of mathematics.  For example, many teachers in high schools use origami to teach many topics in their curriculum.  Areas included are problem solving, geometry, ratios, angles. logic, proofs, congruence, properties of parallel lines, and the list goes on. (Serenevy, 2003).  One example Robert Lang gave in his TED talk was the fact that any origami figure can be unfolded and colored using only 2 colors.  This would be a good example to show in a discrete mathematics class in high school (INSERT CITATION).  There is also a fairly obvious connection to the field of geometry.  Many geometric shapes and designs can be made with one sheet of square paper using different folds.  Overall, even though the mathematics is starting to have a much deeper role in the creation of origami figures, there is a practical use for this math at a high school level relating to several different mathematical fields.  

Importance of Origami Groups

    -What are they used for?
-Who uses this math?
-Practicality

Examples

  The following are examples of origami figures as well as their crease patterns.

 Flag from 1 sheet of paper


Crease Pattern for the Flag above

Frog created from 1 sheet of paper

Crease pattern for the frog origami above

Spider Created from one sheet of paper

Crease pattern for spider origami above

Interesting Links

-The following is a TED Talk given by Robert Lang discussing how interesting origami figures can be constructed thanks to particular mathematical rules.

     http://www.ted.com/talks/robert_lang_folds_way_new_origami.html?quote=323

References

Aharoni, G. (2013).  Origami swans.  Retrieved from http://www.giladorigami.com/PG_Swans.html

PBS.  (Nov. 30, 2009).  Between the folds.  Retrieved from http://www.pbs.org/independentlens/between-the-folds/history.html

Serenevy, A. K.  (Feb. 2003).  Where's the math in origami?  Retrieved from http://math.serenevy.net/?page=Origami-WhereMath

Robert J. Lang (2004-2013) "Eyeglass Telescope" http://www.langorigami.com/science/technology/eyeglass/eyeglass.php