Contents
The County Problem - A Topological Argument
keyword: tutorial, inside county, closed curve, curve
INTRODUCTION In this tutorial / exploration, I'll talk a little about topology, and a little about programming, with the goal of showing you that thinking mathematically can really get you out of a pickle sometimes.
Contents - The Problem - The Solution - Why it works - References
The problem
I'd like to construct a function in some computer language which I can send a latitude and longitude and receive back:
The problem we want to solve here is as follows: we want to create a computer function which takes an Indiana longitude and latitude value as input, and returns the county in which this point lies. At first this seems like a rather simple problem, for when one looks at a county and some point inside the county, they can immediately see whether the point is inside the county. For example, in Java we would want:
String getCounty( float lat, float lon ) {
//Code here
}
System.out.println( getCounty( 39.162147, -86.529045 ) );
to output "Monroe", because that (39.162147, -86.529045) is in Monroe county.
The solution
The solution here is due to a rather fun and at first surprising topological fact. Imagine we have some closed, simple curve in the plane. Here, closed just means that the two ends of the curve meet, and simple means that this curve doesn't intersect itself. In mathematical terms, the curve can be parameterized by a function
$ f: [0, 1] \to \mathbb{ R } $
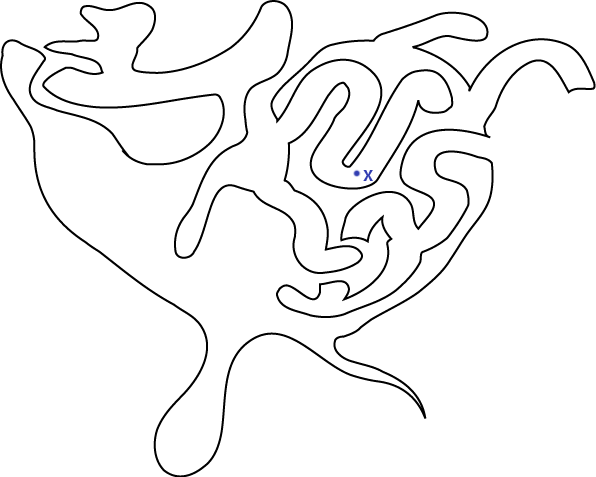
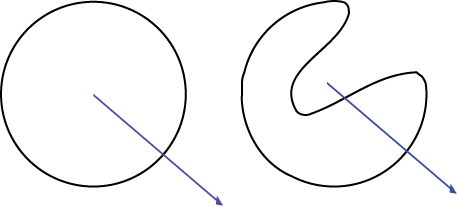
which is continuous (this is what makes it a curve), invective on $ [0, 1) $ (this is what makes it simple), and $ f(0) = f(1) $ (this is what makes it closed). This is called a Jordan Curve. Intuitively, we can think of a Jordan curve as anything we could make with a loop of string on a table, without letting it cross itself. The remarkable fact is that if you have any Jordan curve, which can get pretty complicated, and some point of interest which you'd like to determine whether the point is inside or outside this curve, it's quite simple. Let's say we're interested in the curve below:
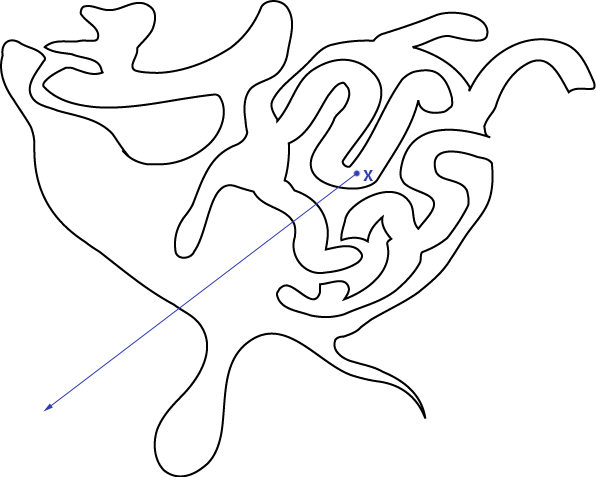
and we'd like to know whether x is inside or outside the curve. Just draw a ray from that point in any direction and count the number of times it intersects the curve:
If the ray intersects the curve an odd number of times, the point is inside. If the number of intersections is even, the point is outside. We can see here that it intersects the sides an even number of times, and we can confirm visually that the point x is indeed outside the curve. That's it! You can easily do some testing of this by drawing crazy Jordan curves (make sure they are both simple and closed) and a random point, and trying to determine the "insideness" of the point. I'll explain in the next section why this statement is true, and maybe you can convince yourself of it if you do some mindful fiddling with Jordan curves. But now I'll show you how we can implement this and solve the original problem.
Now, the first
Why it works
- Explain what a homeomorphism is
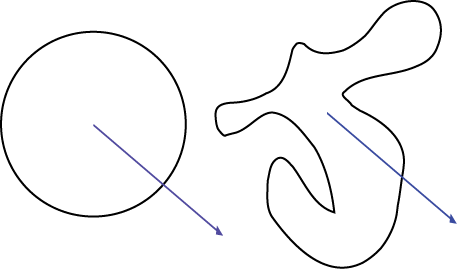
Now why does this work? It seems like a magical fact which I just pulled out of my pocket. But the great thing about this particular mathematical fact is that it's something which we can easily argue. So here I'll present the outline of a proof. The idea is that if we were to take a large circle, we can bend continuously, and with rather strict rules, into an arbitrary simple, closed curve (a curve which is simple and curved is commonly called a Jordan Curve). These strict rules preserve a specific property of the curve which corresponds to the insideness of the chosen point.
Imagine you start with some arbitrary curve in the plane, and you're interested in whether a point is inside or outside the curve:
Now imagine you draw a ray from that point in an arbitrary direction in the plane, and that we focus on the number of intersections that line makes with the sides or the curve:
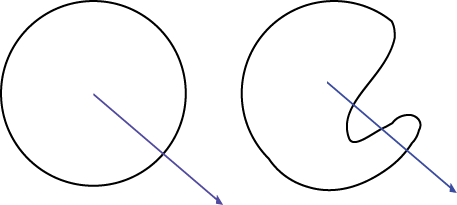
It is not yet clear what the relationship is between the number of intersections and the insideness of the point, but we can try to reduce the situation to a simpler situation. Imagine the various deformations of the curve which preserve insideness and the effect these has on the number of intersections:
//Copied out of here
Note then that the first two homeomorphisms and the inverse of the second preserve insideness. Because every Jordan curve is homeomorphic to the unit circle, we know there exists a homeomorphism between the two, and it is easy to see that this homeomorphism can be broken down into type 1, type 2, type 3, and the inverse of type 2 and type 3 homeomorphisms.
Theorem:
A point is inside a closed curve ""if and only if"" any ray going away from this point intersects the curve an odd number of times.
Outline of proof:
First note that every closed simple loop, or Jordan curve is homeomorphic to the unit circle. Then it easily follows that given an arbitrary curve in the plane, and a point within it, there exists a "smooth transformation" of the curve into the unit circle about that point. This is evident because given some coordinate system, there exists a smooth mapping between the curve and the unit circle, and there then exists a linear transformation of this unit circle about the origin into a unit circle about the point in question.
Once we are aware that there exists this smooth transition we can focus on how this property, the number of intersections of a ray with the curve, changes with time t. The trick is that there are only finitely many states of the homeomorphism in [0, 1] on which the intersection number changes. We are able to characterize these as follows:
Type 1: A homeomorphism which preserves both number of intersections and insideness
Type 2: A homeomorphism which preserves insideness, but not number of intersections
Type 3: A homeomorphism which preserves neither number of intersections or insideness
I will denote these functions as $ T_{i} $ and their inverses, also homeomorphisms by definition, by $ T^-1_{i} $. Then intuitively you can convince yourself that any homeomorphism can be illustrated as a combination of these six functions (five if you account that $ T_{i} = T^-1_{i} $) in sequence. The rigorous proof of this fact involves differential geometry, but if you can convince yourself that this is true for the string analogy, that's all you need to convince yourself this is true in any real life situation. So let's introduce some notation that'll be helpful. We have some continuous series of functions, $ f_{t}: [0,1) \to \mathbb{R}^2 $, which represents the homomorphism between the given curve and the unit circle centered about the point in question.
REFERENCES
[1] "Loream Ipsum" <http://www.lipsum.com/>.