The Cantor set is a famous set first constructed by Georg Cantor in 1883. It is simply a subset of the interval [0, 1], but the set has some very interesting properties. We will first describe how to construct this set, and then prove some interesting properties of the set.
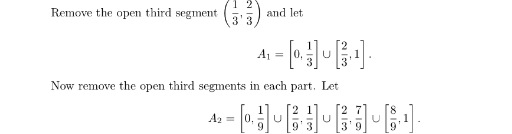Continue in this way always removing the middle third of each segment to get A3,A4, . . ..
Note that A1 ⊇ A2 ⊇ A3 ⊇ · · · . And for each k ∈ N, Ak is the union of 2k closed intervals, each of length
3−k.
Let C = ∩1
i=1Ai. Then C is the Cantor set.
Now we will prove some interesting properties of C.
[Category:MA375Spring2012Walther]
