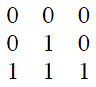Quiz Questions Pool for Week 14
Q1. Assume we know (or can measure) a function
$ \begin{align} p(x) &= \int_{-\infty}^{\infty}f(x,y)dy \end{align} $
Using the definition of the CSFT, derive an expression for F(u,0) in terms of the function p(x).
Q2. Consider the following 2D system with input x(m,n) and output y(m,n)
$ y(m,n) = x(m,n) + \lambda \left( x(m,n) - \frac{1}{9} \sum_{k=-1}^{1}\sum_{l=-1}^{1}x(m-k,n-l) \right) $
a. Is this a linear system? Is it space invariant?
b. What is the 2D impulse response of this system?
c. Calculate its frequency response H(u,v).
d. Describe how the filter behaves when $ \lambda $ is positive and large.
e. Describe how the filter behaves when $ \lambda $ is negative and bigger than -1.
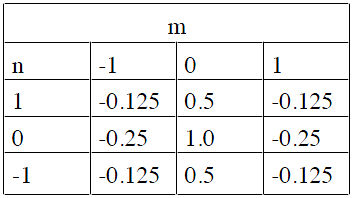
Q3. Consider a 3 * 3 FIR filter with coefficients h[m, n]
a. Find a difference equation that can be used to implement this filter.
b. Given an input image, find the center pixel value of output image.
c. Find a simple expression for the frequency response (DSFT) H(u,v) of this filter.
Q4. Consider the following discrete space system with input x[m,n] and output y[m,n]given by
$ y[m,n]=x[m,n]+\frac{1}{2}y[m+1,n-1] $
Compute the transfer function
$ H(z_1 ,z_2)=\frac{Y(z_1 ,z_2)}{X(z_1 ,z_2)} $
Back to ECE 438 Fall 2010 Lab Wiki Page
Back to ECE 438 Fall 2010