Post Lecture Speech notes

Basic Idea

• Speech is an acoustic signal, which we approximate as an analog signal. It is our goal to change this analog signal into a digital so that we can perform various forms of processing on it.

Parts of Speech

• Before we jump into the mathematical "deep end" we first need to know the basic building blocks of speech

• A sentence that we hear is made up of syllables (sound) and separations (no sound). Simply put, a syllable is a single, uninterrupted sound that forms the rhythmical foundation of a language. For example, the word 'water' has two syllables, 'wa' and 'ter' separated by a tiny break in speech.

• If we go down further, each syllable is formed of phonemes. A phoneme is the smallest, segmental unit of sound. It is what forms the difference between utterances. Even though two different groups use the same language and have different accents and because the phonemes have the same function.

• Since phonemes are the smallest block of a speech signal, it is no surprise that they form the basis for speech analysis.

Phonemes

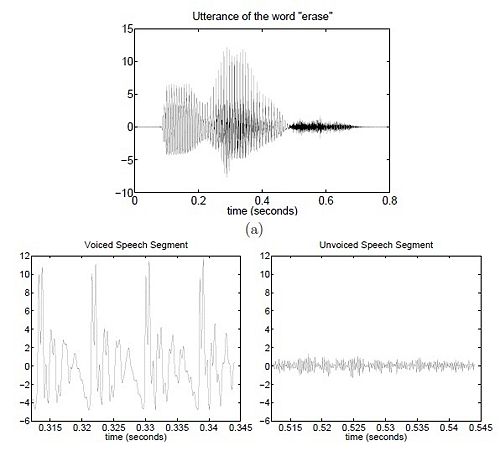
There are two types of phones, voiced and unvoiced.

• Voiced phonemes consist of all vowels and some consonants whereas unvoiced phonemes are just consonants.

There are two methods to differentiate between the two when observing the time domain plot of the audio signal

1) Average Power: By comparing the average power $ P = \frac{1}{L} \sum_{n=1}^L x^2(n) $.

• $ P_{avg,voiced} > P_{avg,unvoiced} $

2) Zero-crossings: Alternatively, you can compare how many times the signal crosses the zero-axis.

• Zero crossing (Unvoiced) > Zero crossing (Voiced)

Since the voiced section is approximately period, it can be modeled as a pulse train. Similarly, the unvoiced section can be modeled as white noise.

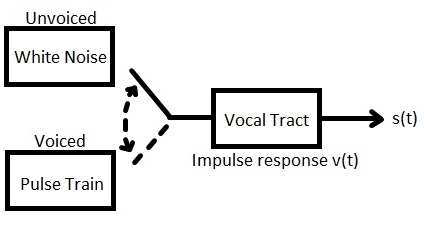
Modeling of Speech Production

Utilizing this valuable information we can now construct a model for speech production as shown below.

where $ s(t) = x(t) \ast v(t) $ where x(t) is the excitation (either pulse train or white noise)

prelecture notes here SupplementarySpeech_prelecture