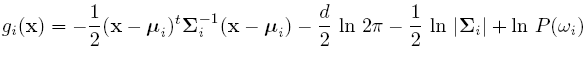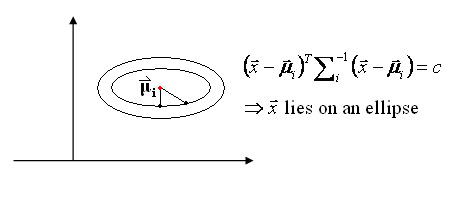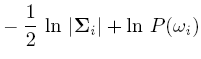LECTURE THEME : - Discriminant Functions
Discriminant Functions: one way of representing classifiers
Given the classes $ \omega_1, \cdots, \omega_k $
The discriminant_OldKiwi functions $ g_1(x),\ldots, g_K(x) $ such that $ g_i(x) $ n-dim S space $ \rightarrow \Re $
which are used to make decisions as follows:
decide $ \omega_i $ if $ g_i(x) \ge g_j(x), \forall j $
Note that many different choices of $ g_i(x) $ will yield the same decision rule, because we are interested in the order of values of $ g_i(x) $ for each x, and not their exact values.
For example: $ g_i(x) \rightarrow 2(g_i(x)) $ or $ g_i(x) \rightarrow ln(g_i(x)) $
In other words, we can take $ g_i(x) \rightarrow f(g_i(x)) $ for any monotonically increasing function f.
Relation to Bayes Rule
e.g. We can take $ g_i(\mathbf(x)) = P(\omega_i|\mathbf(x)) $
then $ g_i(\mathbf(x)) > g_j(\mathbf(x)), \forall j \neq i $
$ \Longleftrightarrow P(w_i|\mathbf(X)) > P(w_j|\mathbf(X)), \forall j \neq i $
OR we can take
$ g_i(\mathbf(x)) = p(\mathbf(x)|\omega_i)P(\omega_i) $
then $ g_i(\mathbf(x)) > g_j(\mathbf(x)), \forall j \neq i $
$ \Longleftrightarrow g_i(\mathbf(x)) = ln(p(\mathbf(x)|\omega_i)P(\omega_i)) = ln(p(\mathbf(x)|\omega_i))+ln(P(\omega_i) $
OR we can take
$ g_i(\mathbf(x)) = ln(p(\mathbf(x)|\omega_i)P(\omega_i)) = ln(p(\mathbf(x)|\omega_i))+ln(P(\omega_i) $
We can take any $ g_i $ as long as they have the same ordering in value as specified by Bayes rule.
Some useful links:
- Bayes Rule in notes: https://engineering.purdue.edu/people/mireille.boutin.1/ECE301kiwi/Lecture4
- Bayesian Inference: http://en.wikipedia.org/wiki/Bayesian_inference
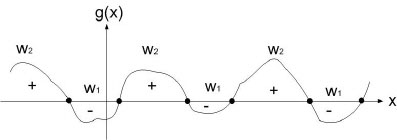
Relational Decision Boundary
Ex : take two classes $ \omega_1 $ and $ \omega_2 $
$ g(\vec x)=g_1(\vec x)-g_2(\vec x) $
decide $ \omega_1 $ when $ g(\vec x)>0 $
and $ \omega_2 $ when $ g(\vec x)<0 $
when $ g(\vec x) = 0 $, you are at the decision boundary ( = hyperplane)
$ \lbrace \vec x | \vec x \;\;s.t \;\;g(\vec x)=0\rbrace $ is a hypersurface in your feature space i.e a structure of co-dimension one less dimension than space in which $ \vec x $ lies
Discriminant function for the Normal Density
Suppose we assume that the distribution of the feature vectors is such that the density function p(X|w) is normal for all i.
Eg: Length of hair among men is a normal random variable. Same for hairlength in women. Now we have:
is the Mahalanobis Distance Squared from X from mui
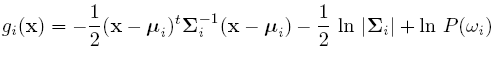
For simplicity, add n/2ln(2pi) to all gi's. Then we get:
Prior Term:
If classes are equally likely, then we can get rid of the first term.
If the Distribution Matrix is the same, then the second term goes off.
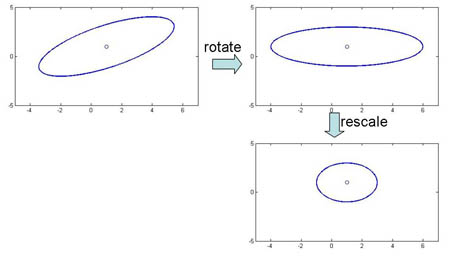
Special case 1: "Spherical clusters" in n-dimensional space. Equidistant points lie on a circle around the average values.
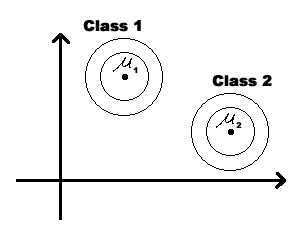Figure 3
Final Note on Lecture 5:
We could modify the coordinates of a class feature vector (as shown on the figure below) to take advantage of Special Case 1. But you should be aware that, in general, this can not be done for all classes simultaneously.
Figure 4
Figure 5
