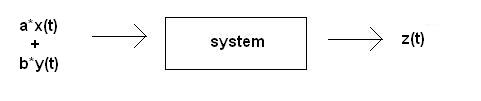
Basics of Linearity
We are given the following information:
- For input $ x(t) = e $ (2jt) the output $ y(t) = te $(-2jt).
- For input $ x(t) = e $ (-2jt) the output $ y(t) = te $(2jt).
- The system is Linear.
We can break down the input $ \,\ x(t) = cos(2t) $ into $ \,\ x(t) = \frac{1}{2} * (e $(j2t) $ \,\ + e $(-j2t)$ \,\ ) $.
Now we can use the property of linearity to determine the output.