Part 1: DT Signals From one CT Signal
In this example, I will use the CT signal I demonstrated in homework 1.4, $ sin(x) $, to create two DT signals. One signal will be periodic, and the other will not.
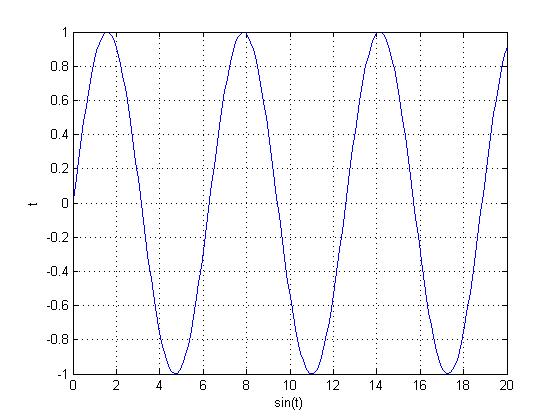
Here is the original function, $ sin(x) $
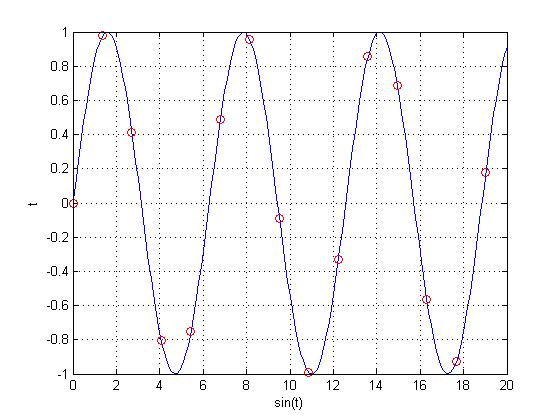
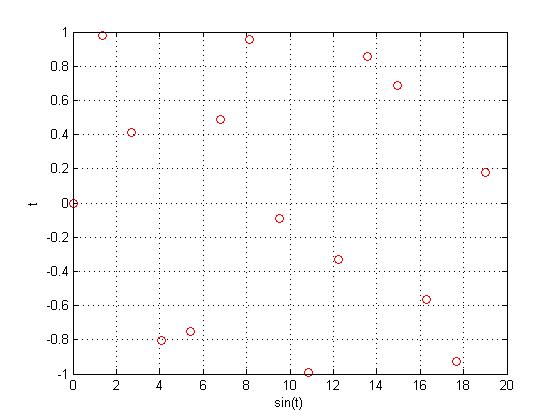
There is very little chance of accidentally getting a periodic DT signal from $ sin(x) $. Choosing some arbitrary number, we will sample $ sin(x) $ at $ \frac{e}{2} $, giving us $ x[n]=sin(\frac{e}{2}n) $. The graph of this function looks like this:
Taking out the original function $ sin(x) $, we can see that there is no pattern to the function with a sample rate of $ \frac{e}{2} $, meaning the function is not periodic.
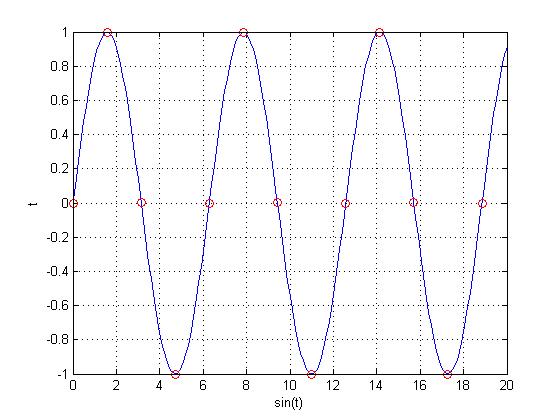
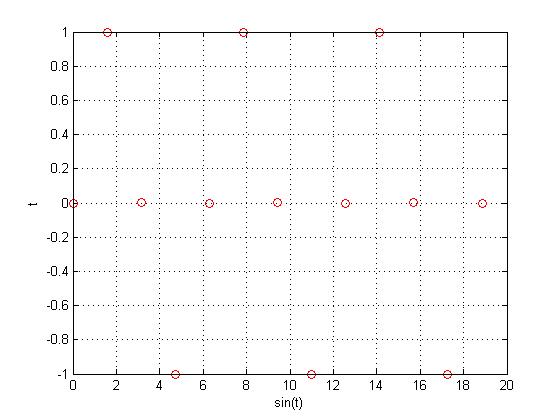
Now, let's replace that $ \frac{e}{2} $ with $ \frac{\pi}{2} $ and see if we can come up with a periodic function.
Above is the function $ x[n]=sin(\frac{\pi}{2}n) $, and if you can't see the pattern, below is the function without the underlying CT function $ sin(x) $.
As you can see from the above graph, there is a clear pattern in the function $ x[n]=sin(\frac{\pi}{2}n) $, meaning that it is periodic.