Time Invariance
A system is time-invariant if for any input $ x(t)\! $ and any $ t_0\! $ (where $ t_0\! $ is a real number) the response to the shifted input $ x(t-t_0)\! $ is $ y(t-t_0)\! $.
One can show a system is time invarient by proving
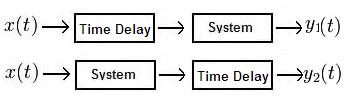
where $ y_1(t)\! $ and $ y_2(t)\! $ are equal.
Example of a Time Invariant System
Let $ y(t)=2x(t)\! $. The system is time invarient if for input $ x(t-t_0)\! $ the response is $ 2x(t-t_0)\! $.
Proof:


