Symmetries in Crystal Structure
Introduction of Crystal structure
The solid substances existing in nature can be divided into two categories: crystalline and amorphous. The essential difference between crystalline and amorphous structures is how the atoms, ions, molecules, and other particles that make up the structures are arranged. Crystals are regularly arranged (long program), while the particles in amorphous substances are stacked together irregularly (short program). In the field of crystallography, researchers study the symmetry of crystal structures in order to perform data collection and categorize substances. However, an understanding of the group structure needs to be added to the chemistry-only approach to crystallography. Through group theory and rigid motion analysis, mathematics allows us to organize crystal structures.
When tasked with classifying a crystal structure, a chemist and a mathematician would approach this problem very differently. A chemist would memorize what a crystal structure would look like and associate that directly with a type of crystal. On the other hand, a mathematician would classify a crystal structure according to group theory. Instead of relying on memory, group theory allows one to "solve" a crystal's structure.
How Symmetry is used to Categorize Crystals
Crystals are a classification of solids with a 3-dimensional order. Any solid with a well-defined atomic pattern visible on its surface is a crystal. There are often several observations that suggest a structure is crystalline without using some diffraction experiment or other advanced procedures. Typically, crystals have flat faces and sharp edges, alongside one or more directions that can be cleaved cleanly. Structures that have a round shape or curves are often described as "glass" due to not having a 3-D order.
When you look at several crystals from the same material, you will notice that they all share the same shape, in particular the angles will be the same. This observation was made by Nicholas Steno in 1669, and is known as the law of constancy of interfacial angles.
Steno and other scientists in the 17th century believed that crystals must be made of some regularly-repeating components. By analysing crystals of calcite, which were built from many small blocks, René-Just Haüy was able to postulate that blocks could easily be used to describe the faces of these crystals. This is known as the law of rational indices.

Having a well-defined pattern means that the crystals have translational symmetry. This means you can take an internal piece of a crystal and translate it, which will perfectly overlap another section of the crystal. The core principle of crystal symmetry is that the pieces must be translationally symmetric.
The use of Group Theory for Classification
Group theory addresses how a certain collection of mathematical “objects,” in this case, crystals, are related. Each crystal structure has its own group of rigid motions that can be applied while preserving translational symmetry, allowing us to categorize them. For group theory, we also require an operation that can be applied to the elements of a group and elements. An element would be a rigid motion that preserves translational symmetry, and the operation is a composition of two elements. For instance, take the first element, apply it to the structure, then apply the second element. This is the same as applying the composition of the first and second elements of the group to the structure.
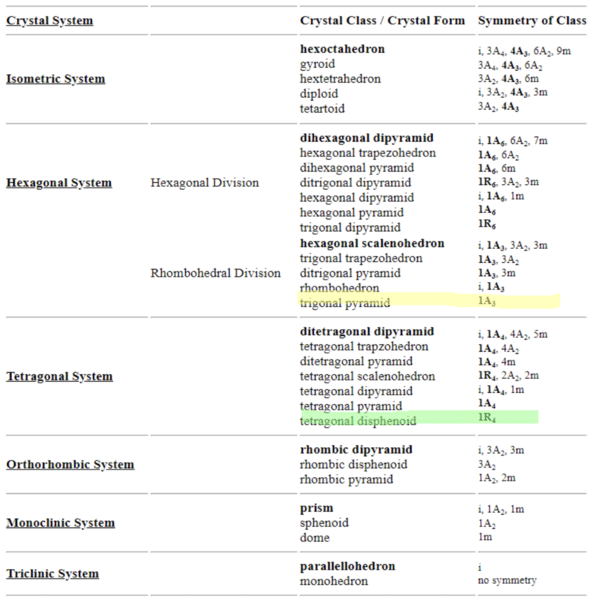
There are also classifications of these groups. For instance, if there is a 4-fold rotational axis in the crystal structure, which means that it has an axis with four rotations that preserve translational symmetry, then that means that the crystal is a tetragonal system. Other classifications of crystal symmetry groups are isometric, hexagonal, orthorhombic, monoclinic, and triclinic. In total, there are 32 known crystal classes.
By identifying the various symmetry operations on a structure (such as rotation, reflection,...), scientists are able to categorize samples into one of the 32 different classes.
2D Symmetry
For 2D Structures, as we learned in Chapter 11, the three types of symmetry operations are rotation, reflection, and inversion.
- Our notation for rotational symmetry is An where n denotes the number of folds.
- A mirror plan (or mirror symmetry) - gives the exact reflection on other side of the plan: same distance, same component/atoms/molecules. This symbolized with the letter "m" and with a solid line.
- A center of symmetry - is an inversion through a point, symbolized with the letter "i". In 2D, a center of the symmetry and a
2‐fold rotation axis have the same effect
- Glide Translation - Translation + Mirror
Ethics in Crystallography
Crystallography is often used in novel research, and our understanding of crystals is constantly improving. Also, almost any material can be crystalized, so crystallography applications are widespread. Moreover, the classification of crystals, which is what we are doing by analyzing crystal symmetry, is essential because many properties of crystals are determined by what groups they fall under or what types of symmetry they have. Crystallography has often been used to find important information about the world around us, such as the applications of x-rays, the discovery of penicillin, or the way DNA replicates.
Many people believe that the next steps in scientific discovery lie behind the discovery of new materials with more desirable properties. This is important to crystallography because the symmetry groups of a crystal affect its tensor groups, which describe a material’s physical properties. With that in mind, crystallography will continue to be a critical area of study in the near future. With the many benefits of crystallography research, it is hard to find enough downsides to outweigh the interest in the area. However, a couple of problems arise, such as the legitimacy of synthesized crystals, the environmental impact of crystal mining, and how crystal synthesizing affects job availability in different parts of the world.
While synthesized crystals have been proposed as an alternative to mined crystals for uses such as jewelry, many people oppose the notion of lab-made crystals and gems. Some people refuse to buy synthesized crystals because they mean less or are less legitimate, while others say it is unethical. The reliance on synthesizing crystals can take away jobs and devastates communities that depend on mining as the primary driver of their economies. On top of that, synthesizing crystals produces more CO2 emissions than mining does. So the positive impact on the environment is still under debate. However, the mining industry has recently declined due to publications and movies about the unethical practices of many mining companies, such as child labor, terrible pay, and dangerous working conditions. Thus, whether ethical or not, we are seeing a steadily growing percentage of crystals made in labs rather than mined.
Source
https://sgp.fas.org/othergov/doe/lanl/pubs/00326655.pdf
http://xrayweb.chem.ou.edu/notes/symmetry.html
http://sarahlambart.com/teaching/mineralogy-03.pdf
https://www.iop.org/explore-physics/big-ideas-physics/crystallography#gref
https://www.worldatlas.com/articles/what-is-the-environmental-impact-of-the-mining-industry.html
https://opengeology.org/Mineralogy/10-crystal-morphology-and-symmetry/