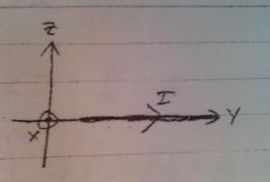
2)
Biot-Savart:
$ \begin{equation*} d\bar{H}=\frac{I(\bar{R})d\bar{l}\times(\bar{R}-\bar{R}')}{4\pi|\bar{R}-\bar{R}'|^3} \end{equation*} $
$ \begin{align*} \bar{R}&= 0\hat{x}+0\hat{y}+0\hat{z}\\ \bar{R}'&=y\hat{y}\\ |\bar{R}-\bar{R}'|&=y \\ d\bar{l}&= (dy)\hat{y} \end{align*} $
$ \begin{equation*} d\bar{H}=\frac{(Idy)\hat{y}\times(-y\hat{y})}{4\pi|y|^3}=0 \longrightarrow \boxed{\bar{H}=0} \end{equation*} $
$ \begin{align*} \text{\underline{Ampere}:}& & \nabla\times\bar{H}&=\bar{J} & &\longrightarrow& & \oint \bar{H}\cdot d\bar{l}&=I_{enc}\\ \text{at the origin:}& & I_{enc}&=0 & &\longrightarrow& & \boxed{\bar{H}=0} \end{align*} $