1)
a)
$ P_{ave} = \int\frac{1}{2}Re[\bar{E}\times\bar{H}^*]d\bar{s} \left\{ \begin{array}{ll} A:area\\ n_0 = \sqrt{\frac{\mu_0}{\epsilon_0}} \end{array} \right.\\ $
for TEM: $ P_{ave} = \frac{1}{2n_0}|E|^2(A) $\\
$ P_{ave} = \frac{1}{2n_0}|E|^2(0.02)(0.001)=10W\\ |E| = \sqrt{\frac{20n_0}{2\cdot10^{-5}}} = \sqrt{10n_0 10^5}\\ |E| =10^3\sqrt{n_0} $
b)
$ R_s =\frac{1}{\sigma\delta} = \frac{P}{\delta} = P\sqrt{\pi f\mu\sigma} = P\sqrt{\frac{\pi f \mu}{P}} = \sqrt{P\pi f \mu} P = 10^{-5}\Omega\cdot m R_s = \sqrt{(10^{-5})\pi(10^9)\mu_0} = \sqrt{\pi\mu_0 10^4} R_s=100\sqrt{\pi\mu_0}\Omega $
c)
$ P_{ave_d} = \frac{1}{2}\int\sigma E^2dv $
\underline{Note}: field is only near the surface\\
$ J_s =\sigma E_s \begin{align*} P_{ave}& = \frac{1}{2}|J_s|^2R_s(A)\\ & = \frac{\sigma^2}{2}|E|^2R_s(0.1)(0.02)\\ & = \frac{\sigma^2}{2}(10^6)n_0R_s(0.1)(0.02)\\ & = \frac{n_0\sigma^2}{2}(100)\sqrt{\pi\mu_0}(0.002)\\ & = \frac{n_0\sigma^2\sqrt{\pi\mu_0}}{10}\\ \end{align*} $
2)
Note: See useful equations.
a)
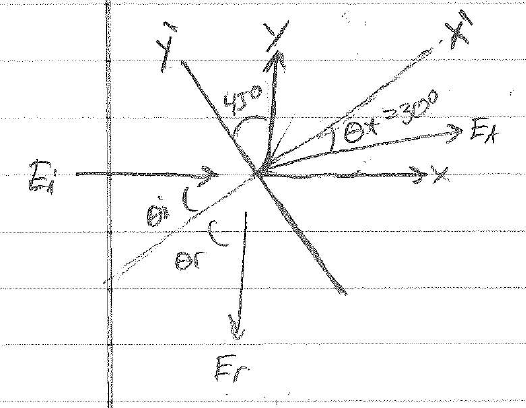
$ \bar{H}_i = \frac{E_0}{n_0}e^{-j\beta_0x}(-\hat{y}) = \sqrt{\frac{\mu_0}{\epsilon_0}}E_0e^{-j\beta_0x}(-\hat{y}) $
b)
$ \bar{P} = \bar{E}\times\bar{H} \bar{P}_{ave} = \frac{1}{2}Re[\bar{E}\times H^*] = \frac{E_0^2}{2n_0}\hat{x} = \text{ (times - average PV)} \bar{P} = \frac{E_0^2}{n_0}e^{-2j\beta_0x}\hat{x} = \sqrt{\frac{\mu_0}{\epsilon_0}}E_0e^{-2j\beta_0x}(\hat{x}) $
c)
TE: $ \Gamma = \frac{\frac{n_2}{\cos\theta_t}-\frac{n_1}{\cos\theta_i}}{\frac{n_2}{\cos\theta_t}+\frac{n_1}{\cos\theta_i}} = \frac{n_2\cos\theta_i-n_1\cos\theta_t}{n_2\cos\theta_i+n_1\cos\theta_i}\leftarrow \text{also can get from useful eqns,} n_1\sin\theta_i = n_2\sin\theta_t \theta_t = \sin^{-1}\bigg(\frac{1}{\sqrt{2}}\sin(45)\bigg) = \sin^{-1}\bigg(\frac{1}{\sqrt{2}}\frac{\sqrt{2}}{2}\bigg)=\sin^{-1}\bigg(\frac{1}{2}\bigg) =30^\circ = \theta_t $
$ \begin{align*} \Gamma &=\frac{n_2\cos(45) - n_1\cos(30)}{n_2\cos(45) + n_1\cos(30)} = \frac{\sqrt{\frac{\mu_0}{2\epsilon_0}}\big(\frac{\sqrt{2}}{2}\big)-\sqrt{\frac{\mu_0}{\epsilon_0}}\big(\frac{\sqrt{3}}{2}\big)}{\sqrt{\frac{\mu_0}{2\epsilon_0}}\big(\frac{\sqrt{2}}{2}\big)+\sqrt{\frac{\mu_0}{\epsilon_0}}\big(\frac{\sqrt{3}}{2}\big)}=\frac{\frac{1}{2} - \frac{\sqrt{3}}{2}}{\frac{1}{2} + \frac{\sqrt{3}}{2}} = \bigg(\frac{1-\sqrt{3}}{1+\sqrt{3}}\bigg)\\ &= \frac{(1-\sqrt{3})(1+\sqrt{3})}{1+2\sqrt{3}+3} = \frac{1-3}{4+2\sqrt{3}} = \frac{-1}{2+\sqrt{3}}\\ \bar{E}_r &= E_0\bigg(\frac{1-\sqrt{3}}{1+\sqrt{3}}\bigg)e^{+j\beta_0y}\hat{z} \end{align*} $
d)
$ \Gamma = \frac{2(\frac{n_2}{\cos\theta_t})}{\frac{n_2}{\cos\theta_t} + \frac{n_1}{\cos\theta_i}} = \frac{2n_2}{n_2+\frac{\cos\theta_t}{\cos\theta_i}n_1}\hspace{1cm}\frac{\cos(30)}{\cos(45)} = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3} \Gamma =\frac{\sqrt{\frac{\mu_0}{2\epsilon_0}}}{\sqrt{\frac{\mu_0}{2\epsilon_0}}+\sqrt{3}\sqrt{\frac{\mu_0}{\epsilon_0}}} = \frac{\frac{1}{\sqrt{2}}}{\frac{1}{\sqrt{2}}+\sqrt{3}} = \frac{1}{1+\sqrt{6}} \bar{E}_t = E_0\bigg( \frac{1}{1+\sqrt{6}}\bigg)e^{-j\beta_0(\hat{x}\cos15+\hat{y}\sin15)}\hat{z}\text{ wrong} $
3)
approximate as rectangular waveguide and find cut-off frequency
$ \omega_c\mu\epsilon = \bigg(\frac{m\pi}{a}\bigg)^2+\bigg(\frac{n\pi}{b}\bigg)^2 f_c = \frac{1}{2\sqrt{\mu\epsilon}}\sqrt{\bigg(\frac{m}{a}\bigg)^2 +\bigg(\frac{n}{b}\bigg)^2} a=1.5m\hspace{1cm}\text{ (longer)}\to x b = 0.5m $
lowest order mode: TE$ _{10} $
$ f_c=\frac{c}{2}\sqrt{\bigg(\frac{1}{a}\bigg)^2} = \frac{c}{2a} f_c = \frac{3\cdot10^8}{2(1.5)} = 10^8\frac{1}{5} f_c=0.1GHz \lambda = \frac{c}{f_c} = 2a = 3m $
$ \to $ longest $ \lambda $ is twice the largest dimension.