1)
a)
$ P = \frac{1}{2}\int Re[\bar{E}\times\bar{H}^*]d\bar{s} =\frac{1}{2n_0}|E|^2(A) =10 \text{ TEM} |E| = \sqrt{\frac{20n_0}{A}} = \frac{\sqrt{20n_0}}{\sqrt{(0.02)(0.001)}}= 10^3\sqrt{n_0} $
b)
$ R_s = \frac{1}{\sigma\delta} = \frac{P}{\delta} = P \sqrt{\pi f\mu\sigma} = \sqrt{\pi f\mu P} \hspace{1cm} p=10^{-5}\Omega m R_s = \sqrt{\pi(10^9)\mu_0(10^{-5})} =100\sqrt{\pi\mu_0} $
c)
$ \begin{align*} P_d &=\frac{1}{2} \int\bar{E}\cdot\bar{J}dv = \frac{1}{2} \int \frac{1}{\sigma}|\bar{J_s}|\bigg(\frac{\bar{J_s}}{\delta}\bigg)ds\\ &=\frac{1}{2} |\bar{J_s}|^2 \frac{1}{\sigma\delta}(A) =\frac{1}{2} |\bar{J_s}|^2R_s(A)\\ &=\frac{1}{2} \sigma^2|E|^2 R_s(A) =\frac{1}{2P^2} |E|^2R_s(A)\\ &=\frac{1}{2}(10^{10})(10^6n_0)(100)\sqrt{\pi\mu_0}(0.02)(0.001)\\ &=\frac{1}{2}\sqrt{\pi\mu_0}(10^{18})(2)(10^{-5})n_0\\ &= n_0\sqrt{\pi\mu_0}(10^{13}) \end{align*} $
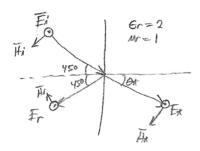
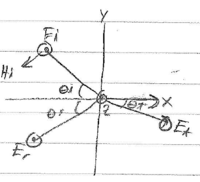
2)
a)
$ \bar{E}_i = \hat{z}E_0e^{-j\beta_0x} \bar{H}_i = (-\hat{y})\bigg(\frac{E_0}{n_0}\bigg)e^{-j\beta_0x} $
b)
$ \bar{P}_i = \bar{E}_i\times\bar{H}_i = \hat{x} \bigg(\frac{E_0^2}{n_0}\bigg)e^{-j2\beta_0x} \text{time-average: } \bar{P}_i = \frac{1}{2}Re[\bar{E}_i\times\bar{H}^*] = \hat{x}\bigg(\frac{E_0^2}{2n_0}\bigg) $
c)
$ Z_{TE} = \frac{n}{\cos\theta} $
$ \begin{align*} n_2&=n_0\frac{1}{\sqrt{2}}\\ n_1&=n_0\\ n_1\sin\theta_i &= n_2\sin\theta_t\\ \frac{1}{\sqrt{2}} = \sin\theta_i &= \sqrt{2}\sin\theta_t\\ \sin\theta_t &= \frac{1}{2}\\ \theta_t &=30^\circ \end{align*} $
$ \begin{align*} \Gamma &= \frac{Z_L - Z_0}{Z_L + Z_0} = \frac{\frac{n_2}{\cos\theta_t} - \frac{n_1}{\cos\theta_i}}{\frac{n_2}{\cos\theta_t} + \frac{n_1}{\cos\theta_i}}\\ \Gamma &= \frac{n_2\cos\theta_i - n_1\cos\theta_t}{n_2\cos\theta_i + n_1\cos\theta_t} = PL\\ \Gamma &= \frac{\frac{1}{\sqrt{2}}\cos(45) - \cos(30)}{\frac{1}{\sqrt{2}}\cos(45)+ \cos(30)} \\ \Gamma &= \frac{\frac{1}{\sqrt{2}}\big(\frac{1}{\sqrt{2}}\big) - \frac{\sqrt{3}}{2}}{\frac{1}{\sqrt{2}}\big(\frac{1}{\sqrt{2}}\big)+ \big(\frac{\sqrt{3}}{2}\big)} =\frac{\frac{1-\sqrt{3}}{2}}{\frac{1+\sqrt{3}}{2}}\\ \Gamma &= \frac{1-\sqrt{3}}{1+\sqrt{3}} \to \bar{E}_r = \hat{z}\frac{(1-\sqrt{3})}{(1+\sqrt{3})}E_0e^{+j\beta y} \end{align*} $
\underline{Note}: Reflected wave travels along $ -\hat{y} $ because $ \theta_i = \theta_r = 45^\circ $
d)
$ \tau = 1+\Gamma = \frac{(1+\sqrt{3}) + (1-\sqrt{3})}{1+\sqrt{3}} = \frac{2}{1+\sqrt{3}} \hat{n}_t = \hat{x}\cos(15^\circ) + \hat{y}\sin(15^\circ) $
e)
$ \bar{E}_t = \hat{z}\bigg(\frac{2}{1+\sqrt{3}}\bigg)e^{-j\beta_0[x\cos(15)+y\sin(15)]} $ transmitted wave propogates at $ 15^\circ $ above x-axis
3)
$ K_c^2 = \omega^2\mu\epsilon = k_x^2 + k_y^2 = \bigg(\frac{m\pi}{a}\bigg)^2 + \bigg(\frac{n\pi}{b}\bigg)^2 f_c = \frac{c}{2}\sqrt{\bigg(\frac{m}{a}\bigg)^2 + \bigg(\frac{n}{b}\bigg)^2 } $ lowest order mode: TE$ _{01} $
$ f_c = \frac{c}{2}\bigg(\frac{1}{a}\bigg) = \frac{c}{2a}=\frac{c}{3} =10^8 = 0.1GHz \lambda_c = \frac{c}{f_c} = 3m $
--- lowest frequency has wavelength of twice the largest dimension.
---assumed rectangular waveguide cut-off frequency applies here.