IMPORTANT: This pages apparently contains scanned pages from a book. Did you check the copyrights of the book before posting? Are you sure this is allowed? In any event, you should always still cite your sources. -Rhea team.
The Cantor set is a famous set first constructed by Georg Cantor in 1883. It is simply a subset of the interval [0, 1], but the set has some very interesting properties. We will first describe how to construct this set, and then prove some interesting properties of the set.
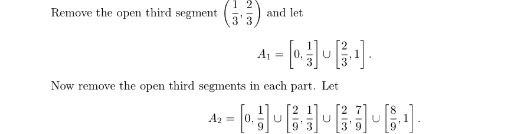Continue in this way always removing the middle third of each segment to get A3,A4, . . ..
Note that A1 ⊇ A2 ⊇ A3 ⊇ · · · . And for each k ∈ N, Ak is the union of 2k closed intervals, each of length
3−k.
Let C = ∩1
i=1Ai. Then C is the Cantor set.
Now we will prove some interesting properties of C.
The term fractal is used to describe objects that cannot be effectively described using normal Euclidean geometry. The word “fractal” is somewhat synonymous with the word “broken”. Below is an example of a well-known fractal object called the Cantor Set. The Cantor Set is created by the following algorithm: Start with the closed interval [0,1]. Call this set ��, or the 0th (initial) set.
You can see the set becomes more sparse the more iterations we perform. The Cantor Set is defined to be the set
of the points that remain as the number of iterations tends to infinity.
If the Cantor Set was composed of discrete points, then every point would be “separate” from every other point.
If this was true, we could enclose any point in the Cantor Set inside a very tiny circle of radius � such that the
circle encloses that one point only. However, we can demonstrate that for any such radius, there will always be
infinitely many other points from the Cantor Set within this circle. For example, we agreed that any point that is
the endpoint of an interval at any iteration remains. So let’s pick x=1/3. This point will never be deleted and is a
member of the Cantor Set. So now let’s pick a small value for delta,say, delta = 1/100
Our claim is that the point x=1/3
And yet, any two points of the Cantor Set are physically separated from one another by at least one deleted
middle-third. So little tiny line intervals do not exist either.
So, we have a case where every point in the Cantor Set is infinitely close to other points within the Cantor Set, yet
no two points in the Cantor Set “touch”, thus segments as we know them do not exist in the Cantor Set. So we
really don’t have segments nor do we have “stand alone” discrete points.
This brings us to Dimension and Fractal Dimension.
The word fractal is roughly translated as “broken” and is used to describe shapes that have a very ragged, broken
appearance to them, that do not lend themselves to the usual notions of Euclidean Geometry. The shape of a
coast line, the outline of a cloud, the “volume” of a swarm of bees, etc. These are not easy to discuss using
normal geometry. (This begs the question, what is “normal” geometry?).
A dimension is simply the number of independent coordinates needed to define the location of a point in some
milieu. For example, a point itself has no dimension – or dimension 0. A line has dimension 1, since you just
need one coordinate to define the location of a point on the line (think of the Real line). Area has dimension 2,
since you need two coordinates to define a point in a “flat region”. Think of our usual (x,y) coordinate axis
system. A volume or spatial region is of dimension 3. In mathematics, higher dimensions are easily handled. The
formula for calculating mortgage payments is a 5-dimensional problem, involving variables “principal”, “time”,
“frequency of payment”, “APR”, and the output “payment”. These are all Euclidean dimensions.
[Category:MA375Spring2012Walther]
