7.7 QE 2003 August
1. (15% of Total)
This question is a set of short-answer questions (no proofs):
(a) (5%)
State the definition of a Probability Space.
Answer
You can see the definition of a Probability Space.
(b) (5%)
State the definition of a random variable; use notation from your answer in part (a).
Answer (74p on Papoulis)
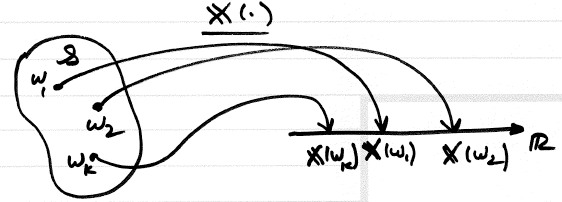
A random variable $ \mathbf{X} $ is a process of assigning a number $ \mathbf{X}\left(\xi\right) $ to every outcome $ \xi $ . The result function must satisfy the following two conditions but is otherwise arbitrary:
1. The set $ \left\{ \mathbf{X}\leq x\right\} $ is an event for every $ x $ .
2. The probabilities of the events $ \left\{ \mathbf{X}=\infty\right\} $ and $ \left\{ \mathbf{X}=-\infty\right\} $ equal 0.
Answer (Intuitive definition)
Given $ \left(\mathcal{S},\mathcal{F},\mathcal{P}\right) $ , a random variable $ \mathbf{X} $ is a mapping from $ \mathcal{S} $ to the real line. $ \mathbf{X}:\mathcal{S}\rightarrow\mathbb{R} $ .
(c) (5%)
State the Strong Law of Large Numbers.
Answer
You can see the definition of the Strong Law of Large Numbers.
2. (15% of Total)
You want to simulate outcomes for an exponential random variable $ \mathbf{X} $ with mean $ 1/\lambda $ . You have a random number generator that produces outcomes for a random variable $ \mathbf{Y} $ that is uniformly distributed on the interval $ \left(0,1\right) $ . What transformation applied to $ \mathbf{Y} $ will yield the desired distribution for $ \mathbf{X} $ ? Prove your answer.
Answer
$ f_{\mathbf{X}}\left(x\right)=\lambda e^{-\lambda x}. $
$ F_{\mathbf{X}}\left(x\right)=1-e^{-\lambda x}. $
| $ y=1-e^{-\lambda x} $ |
| $ e^{-\lambda x}=1-y $ |
| $ -\lambda x=\ln\left(1-y\right) $ |
| $ x=\frac{-\ln\left(1-y\right)}{\lambda} $ |
| $ x=\frac{-\ln y}{\lambda}. $ |
$ \mathbf{X}=F_{\mathbf{X}}^{-1}\left(\mathbf{Y}\right). $
$ F_{\mathbf{X}}^{-1}\left(y\right)=\frac{-\ln y}{\lambda}. $
3. (20% of Total)
Consider three independent random variables, $ \mathbf{X} $ , $ \mathbf{Y} $ , and $ \mathbf{Z} $ . Assume that each one is uniformly distributed over the interval $ \left(0,1\right) $ . Call “Bin #1” the interval $ \left(0,\mathbf{X}\right) $ , and “Bin #2” the interval $ \left(\mathbf{X},1\right) $ .
a. (10%)
Find the probability that $ \mathbf{Y} $ falls into Bin #1 (that is, $ \mathbf{Y}<\mathbf{X} $ ). Show your work.
Solution 1 - Wrong
$ P\left(\left\{ \mathbf{Y}<\mathbf{X}\right\} \right)=\int_{0}^{1}P\left(\left\{ \mathbf{Y}<k\right\} \cap\left\{ \mathbf{X}\geq k\right\} \right)dk=\int_{0}^{1}P\left(\left\{ \mathbf{Y}<k\right\} \right)\cdot P\left(\left\{ \mathbf{X}\geq k\right\} \right)dk $$ =\int_{0}^{1}k\left(1-k\right)dk=\int_{0}^{1}k-k^{2}dk=\frac{1}{2}k^{2}-\frac{1}{3}k^{3}\biggl|_{0}^{1}=\frac{1}{2}-\frac{1}{3}=\frac{1}{6}. $
Solution 2
| $ \int_{0}^{1}\int_{0}^{1}cdxdy=1 $ |
| $ \int_{0}^{1}cdy=1 $ |
| $ c=1 $ |
$ P\left(\left\{ \mathbf{Y}<\mathbf{X}\right\} \right)=\int_{0}^{1}\int_{0}^{x}1dydx=\int_{0}^{1}xdx=\frac{x^{2}}{2}\biggl|_{0}^{1}=\frac{1}{2}. $
b. (10%)
Find the probability that both $ \mathbf{Y} $ and $ \mathbf{Z} $ fall into Bin #1. Show your work.
$ P\left(\left\{ \mathbf{Y}<\mathbf{X}\right\} \cap\left\{ \mathbf{Z}<\mathbf{X}\right\} \right)=\int_{0}^{1}\int_{0}^{x}\int_{0}^{x}1dzdydx=\int_{0}^{1}\int_{0}^{x}xdydx=\int_{0}^{1}x^{2}dx=\frac{1}{3}. $
4. (25% of Total)
Let $ \mathbf{X}_{n},\; n=1,2,\cdots $ , be a zero mean, discrete-time, white noise process with $ E\left(\mathbf{X}_{n}^{2}\right)=1 $ for all $ n $ . Let $ \mathbf{Y}_{0} $ be a random variable that is independent of the sequence $ \left\{ \mathbf{X}_{n}\right\} $ , has mean $ 0 $ , and has variance $ \sigma^{2} $ . Define $ \mathbf{Y}_{n},\; n=1,2,\cdots $ , to be an autoregressive process as follows: $ \mathbf{Y}_{n}=\frac{1}{3}\mathbf{Y}_{n-1}+\mathbf{X}_{n}. $
a. (20 %)
Show that $ \mathbf{Y}_{n} $ is asymptotically wide sense stationary and find its steady state mean and autocorrelation function.
$ \mathbf{Y}_{n}=\frac{1}{3}\mathbf{Y}_{n-1}+\mathbf{X}_{n}=\frac{1}{3}\left(\frac{1}{3}\mathbf{Y}_{n-2}+\mathbf{X}_{n-1}\right)+\mathbf{X}_{n}=\left(\frac{1}{3}\right)^{2}\mathbf{Y}_{n-2}+\mathbf{X}_{n}+\frac{1}{3}\mathbf{X}_{n-1} $$ =\cdots=\left(\frac{1}{3}\right)^{n}\mathbf{Y}_{0}+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}. $
$ E\left[\mathbf{Y}_{n}\right]=E\left[\left(\frac{1}{3}\right)^{n}\mathbf{Y}_{0}+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}\right]=\left(\frac{1}{3}\right)^{n}E\left[\mathbf{Y}_{0}\right]+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}E\left[\mathbf{X}_{n-k}\right] $$ =\left(\frac{1}{3}\right)^{n}\cdot0+\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\cdot0=0. $
$ E\left[\mathbf{Y}_{m}\mathbf{Y}_{n}\right]=\left(\frac{1}{3}\right)^{m+n}E\left[\mathbf{Y}_{0}^{2}\right]+\left(\frac{1}{3}\right)^{m}E\left[\mathbf{Y}_{0}\sum_{k=0}^{n-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}\right] $$ \qquad+\left(\frac{1}{3}\right)^{n}E\left[\mathbf{Y}_{0}\sum_{k=0}^{m-1}\left(\frac{1}{3}\right)^{k}\mathbf{X}_{n-k}\right]+\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}\left(\frac{1}{3}\right)^{i+j}E\left[\mathbf{X}_{m-i}\cdot\mathbf{X}_{n-j}\right] $$ =\left(\frac{1}{3}\right)^{m+n}\cdot\left(\sigma^{2}+0^{2}\right)+\sum_{k=1}^{\min\left(m,n\right)}\left(\frac{1}{3}\right)^{m+n-2k} $$ =\left(\frac{1}{3}\right)^{m+n}\cdot\sigma^{2}+\sum_{k=1}^{\min\left(m,n\right)}\left(\frac{1}{3}\right)^{m+n-2k}. $
$ \because\;\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}\left(\frac{1}{3}\right)^{i+j}E\left[\mathbf{X}_{m-i}\cdot\mathbf{X}_{n-j}\right]=\sum_{i=1}^{m}\sum_{j=1}^{n}\left(\frac{1}{3}\right)^{m-i}\left(\frac{1}{3}\right)^{n-j}E\left[\mathbf{X}_{i}\cdot\mathbf{X}_{j}\right]=\sum_{k=1}^{\min\left(m,n\right)}\left(\frac{1}{3}\right)^{m+n-2k}. $
b. (5%)
For what choice of $ \sigma^{2} $ is the process wide sense stationary; i.e., not just asymptotically wide sense stationary?
5. (25% of Total)
Suppose that “sensor nodes” are spread around the ground (two-dimensional space) according to a Poisson Process, with an average density of nodes per unit area of $ \lambda $ . We are interested in the number and location of nodes inside a circle $ C $ of radius one that is centered at the origin. You must quote, but do not have to prove, properties of the Poisson process that you use in your solutions to the following questions:
a. (10%)
Given that a node is in the circle C , determine the density or distribution function of its distance $ \mathbf{D} $ from the origin.
• $ i)\; d<0,\; F_{\mathbf{D}}\left(d\right)=0. $
• $ ii)\;0\leq d\leq1,\; F_{\mathbf{D}}\left(d\right)=P\left(\left\{ \mathbf{D}\leq d\right\} \right)=\frac{d^{2}\pi}{1^{2}\pi}=d^{2}. $
• $ iii)\;1<d,\; F_{\mathbf{D}}\left(d\right)=1. $
$ \therefore\; F_{\mathbf{D}}\left(d\right)=\begin{cases} \begin{array}{lll} 0 & & ,\; d<0\\ d^{2} & & ,\;0\leq d\leq1\\ 1 & & ,\;1<d \end{array}\end{cases} $
$ f_{\mathbf{D}}\left(d\right)=2d\cdot\mathbf{1}_{\left[0,1\right]}\left(d\right). $
b. (15%)
Find the density or distribution of the distance from the center of $ C $ to the node inside $ C $ that is closest to the origin.
$ \mathbf{X} $ : the random variable for the distance from the center of $ C $ to the node inside $ C $ that is closest to the origin
$ F_{\mathbf{X}}\left(x\right)=P\left(\left\{ \mathbf{X}\leq x\right\} \right)=1-P\left(\left\{ \mathbf{X}>x\right\} \right) $$ =1-P\left(\left\{ \textnormal{no sensor nodes in the circle that has a radius }x\right\} \right) $$ =1-e^{-\lambda x^{2}\pi}. $
$ f_{\mathbf{X}}\left(x\right)=\frac{d}{dx}F_{\mathbf{X}}\left(x\right)=2\lambda x\pi\cdot e^{-\lambda x^{2}\pi}. $