Solution of Week12 Quiz Question 5
a.$ x[n]=cos(\frac{\pi n}{2})\text{ ,n=0,1,2,3} $
$ \begin{align} X[k]&=\sum_{n=0}^3 x[n]e^{-j\frac{2\pi n}{N}k} \\ &=\sum_{n=0}^3 cos(\frac{n\pi}{2})e^{-j\frac{2\pi n}{N}k} \\ &=1-e^{-j\pi k}\text{ , }0\le k\le 3 \end{align} $
b. $ h[n]=2^n\text{ ,n=0,1,2,3} $
$ \begin{align} H[k]&=\sum_{n=0}^3 h[n]e^{-j\frac{2\pi n}{N}k} \\ &=\sum_{n=0}^3 2^ne^{-j\frac{2\pi n}{N}k} \\ &=1+2e^{-j\frac{\pi k}{4}}+4e^{-j\pi k}+8e^{-j\frac{3\pi k}{4}}\text{ , }0\le k\le 3 \end{align} $
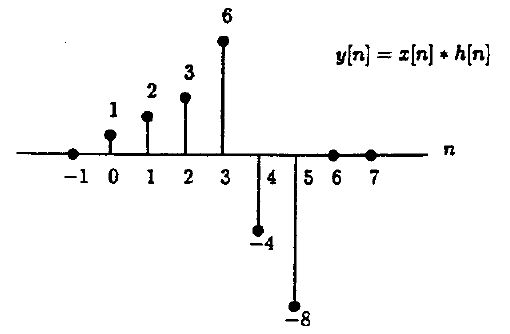
c. Circular convolution equals linear convolution plus aliasing. The length of x[n] is 3 and length of h[n] is 4. We need $ N\ge 3+4-1=6 $ to avoid aliasing. Since N=4, we expect to get aliasing here. First, find y[n]=x[n]*h[n]:
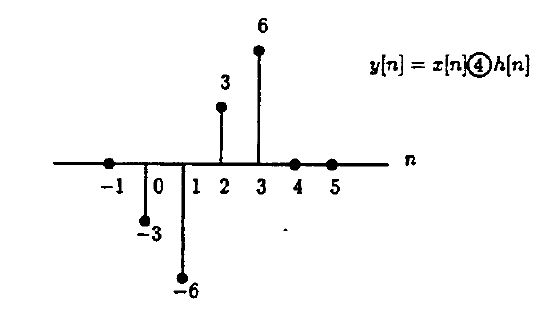
For this problem, aliasing means the last three points (n=4,5,6) will wrap-around on top of the first three points, giving $ y[n]=x[n]\circledast_4 h[n] $
d. Using the DFT values we calculated in parts a and b:
$ \begin{align} Y[k]&=X[k]H[k] \\ &=1+2e^{-j\frac{\pi k}{4}}+4e^{-j\frac{2\pi k}{4}}+8e^{-j\frac{3\pi k}{4}}-e^{-j\frac{2\pi k}{4}}-2e^{-j\frac{3\pi k}{4}}-4e^{-j\frac{4\pi k}{4}}-8e^{-j\frac{5\pi k}{4}} \\ &=-3-6e^{-j\frac{\pi k}{4}}+3e^{-j\frac{2\pi k}{4}}+6e^{-j\frac{3\pi k}{4}}\text{ , }0\le k\le 3 \end{align} $
Taking the inverse DFT:
$ y[n]=-3\delta [n]-6\delta [n-1]+3\delta [n-2]+6\delta [n-3]\text{ , }0\le n\le 3 $