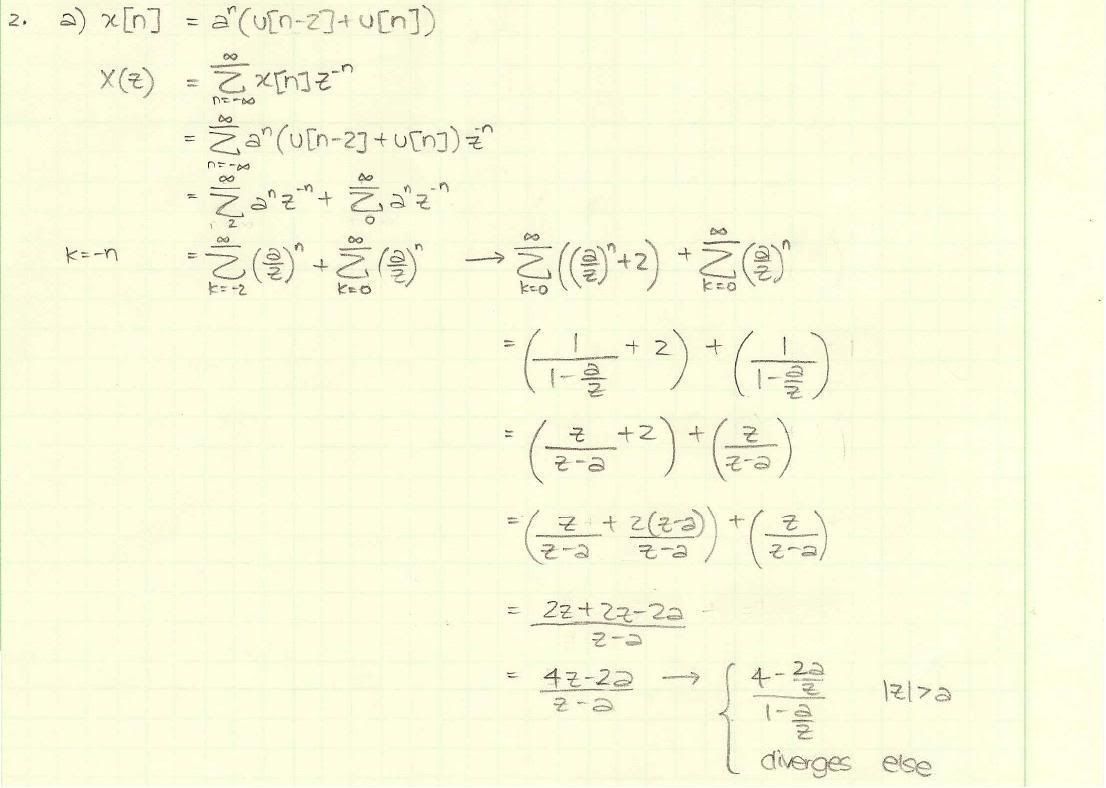I'm not sure if I've done this correctly in the first place. I would like your input before I actually attempt to inverse it.
- Thank you.I tried the LaTeX but it failed miserably.
- Maybe it would be easier if you write it out while you are reading my LaTeX fail trying to help me, otherwise I can come in and see you on Monday.
x[n] = a^n(u[n-2]+u[n])
- X(z)
- = sum[n=-inf,inf] of x[n]z^-n
- = sum[n=-inf,fin] of a^n(u[n-2]+u[n])
- = sum[n=2,inf] of a^n(z^-n) + sum[n=0,inf] of a^n(z^-n)
- Let k = -n
- Therefore, sum[k=-2,inf] of (a/z)^n + sum[k=0,inf] of (a/z)^n
- = sum[k=0,inf] of [(a/z)^n + 2] + sum[k=0,inf] of (a/z)^n
- = (1/1-a/z)+2 + (1/1-a/z)
- = (z/z-a)+2 + (z/z-a)
- = (z/z-a)+(2(z-a)/z-a) + (z/z-a)
- = (4z-2a)/(z-a)
- = (4-2a/z)/(1-a/z) for |z|>a
- EDIT: so if I end up with something that says 1/1-(1/z), I am confused. does it converge when |z|<a or when |z|>a??
- ~ksoong
Answer from Prof. MImi
- In the step where you replaced -n by k, you forgot to replace the n inside the summation. Also, the first sum should then go from -2 to -infinity, instead of infinity.
- Actually, I do not see why you replaced -n by k in both sums. IN the first sum, you should have set k=n-2. In the second sum, you did not need to make any change of variable.
- The arrow in the middle of your computations, and the one towards the end should both be replaced by equal signs.
- The simplification of the first summation following the arrow is incorrect: you would need to add two terms instead of just one.
- The equality following the arrow is only valid when |z|>|a|.You must write this next to the equality!
- This explanation would be much clearer if you had typed in your answer: this way I could make notes directly inside the computations and cross-out and replace stuff using different colors.
Anybody sees anything else? Do you have more questions?