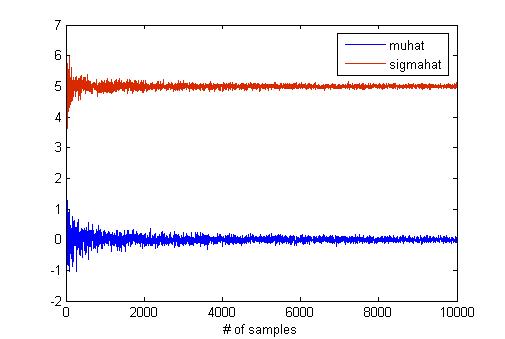
MATLAB has a "mle" function for maximum likelihood estimation. I think that this function is useful to verify the result of hw2 if you have MATLAB. I try to find the effect of the sample size in MLE using "mle" function because the number of samples is critical for estimation. To do this, I generate samples from normal distribution with mean as 0 and std as 5. The below graph shows the results of MLE according to the number of samples.
The code for this graph is like below.
samples_step = 3;
num_samples = samples_step:samples_step:10000;
len = length(num_samples);
mu = 0;
sigma = 5;
muhat = zeros(1, len);
sigmahat = zeros(1, len);
for x = num_samples
data = mu + sigma * randn(1, x);
phat = mle(data(1, :));
muhat(1, x/samples_step) = phat(1);
sigmahat(1, x/samples_step) = phat(2);
end
plot(num_samples, muhat);
hold on;
plot(num_samples, sigmahat);
--Han84 22:49, 2 April 2010 (UTC)
Need real database? Look it up in this website:
http://archive.ics.uci.edu/ml/datasets.html
have fun!
Golsa
Cholesky Decomposition
I wrote this MATLAB / FreeMat code to compute the Cholesky Decomposition of a matrix. The matrix A should be real and positive definite.
function L = cholesky(A)
N = length(A);
L = zeros(N);
for i=1:N
for j=1:i-1
L(i,j) = 1/L(j,j) * (A(i,j) - L(i,1:j-1)*L(j,1:j-1)');
end
L(i,i) = sqrt(A(i,i) - L(i,1:i-1)*L(i,1:i-1)');
end
end
You can use the resulting lower triangular matrix L to generate multivariate normal samples with covariance given by the matrix A by computing
X = $ \mu $ + L Z, where Z is iid standard normal.
Pritchey 20:28, 9 April 2010 (UTC)
Hidden Markov Models
As Prof. Boutin approved my work on HMM for Hw2, I'll put some references for HMM here. For this homework, I'm going to learn the HMM model parameters with the Baum-Welch algorithm, which is a generalized version of EM algorithm. An EM algorithm tries to maximize the likelihood function even though one has variables that cannot be observed. During the implementation, I collected some intuitive tutorials on how to implement the HMM and Baum-Welch algorithm, and will share it here. http://www.indiana.edu/~iulg/moss/hmmcalculations.pdf This is a simple example demonstrating how Baum-Welch runs step by step.
http://www.cs.brown.edu/research/ai/dynamics/tutorial/Documents/HiddenMarkovModels.html This is a good reference on how to name your variables when programming it.
http://www.cs.ubc.ca/~murphyk/Software/HMM/rabiner.pdf This is the classical paper which most of the existing HMM software packages are based on.