(→Periodic Signal) |
(→Periodic Signal) |
||
| Line 22: | Line 22: | ||
However, this still does not fulfill the requirement as <math>N = 2\pi</math> is not an integer. For the signal to become periodic, the CT waveform has to be modified to <math>x(t) = sin(0.5\pi t)</math> and sampled at a frequency of 1 Hz. Upon modification, <math>x[n + 4] = x[n]</math> | However, this still does not fulfill the requirement as <math>N = 2\pi</math> is not an integer. For the signal to become periodic, the CT waveform has to be modified to <math>x(t) = sin(0.5\pi t)</math> and sampled at a frequency of 1 Hz. Upon modification, <math>x[n + 4] = x[n]</math> | ||
| + | |||
| + | <math>x(t) = sin(0.5\pi t)</math> sampled at 1 Hz[[Image:Samp4_ECE301Fall2008mboutin.jpg]] | ||
==Non Periodic Signal== | ==Non Periodic Signal== | ||
Revision as of 08:36, 11 September 2008
Contents
1. Creating two DT signals (one periodic and one non-periodic) from a periodic CT signal
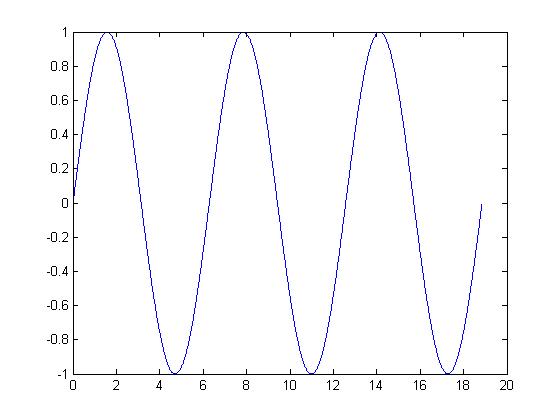
Let $ x(t) = sin (2\pi t), $ which is a periodic CT signal
$ x(t) = sin (2\pi t) $
Sampling every t = 0.01
Periodic Signal
Sampling every $ t = \pi $
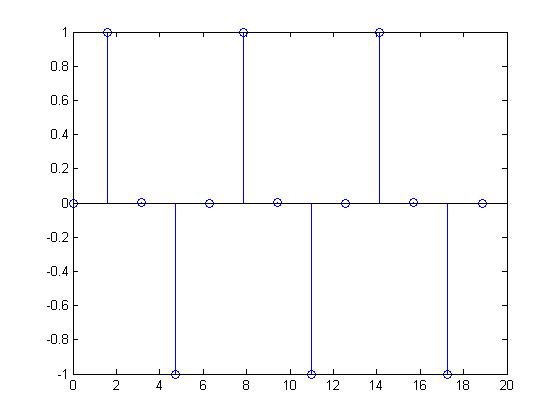
This discrete time signal was produced from a CT sine wave by sampling at a frequency of $ \frac{1}{\pi} $.
As can be seen from the graph, the values of x[n] are periodic because they repeat after every period of $ t = 2\pi $.
Therefore, $ x[n + 2\pi] = x[n] $
However, this still does not fulfill the requirement as $ N = 2\pi $ is not an integer. For the signal to become periodic, the CT waveform has to be modified to $ x(t) = sin(0.5\pi t) $ and sampled at a frequency of 1 Hz. Upon modification, $ x[n + 4] = x[n] $
$ x(t) = sin(0.5\pi t) $ sampled at 1 Hz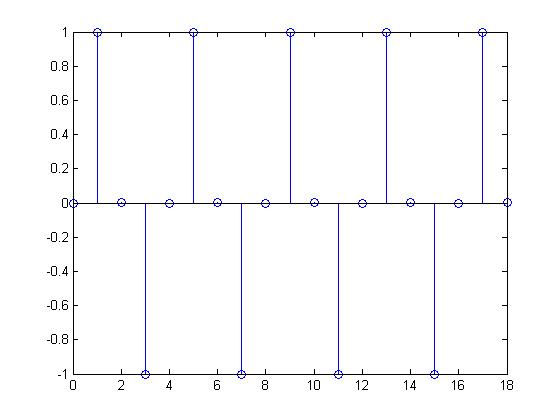
Non Periodic Signal
Sampling every t = 2
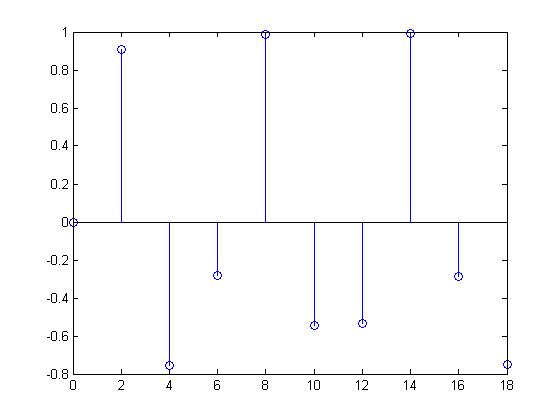
For this discrete time signal which was produced by sampling the same sine wave at a frequency of 0.5, the values of x[n] are non-periodic because the discrete time signal is scattered all over the place with no indication of a pattern. Therefore, $ x[n + k] \neq x[n] $
