(→Periodic Signal) |
|||
| Line 1: | Line 1: | ||
==1. Creating two DT signals (one periodic and one non-periodic) from a periodic CT signal== | ==1. Creating two DT signals (one periodic and one non-periodic) from a periodic CT signal== | ||
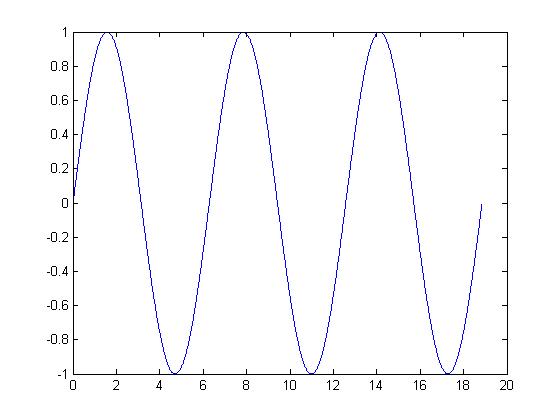
| − | Let x(t) = sin (t), which is a periodic CT signal | + | Let <math>x(t) = sin (2\pi t),</math> which is a periodic CT signal |
| − | + | <math>x(t) = sin (2\pi t)</math> | |
[[Image:Sin1_ECE301Fall2008mboutin.jpg]] | [[Image:Sin1_ECE301Fall2008mboutin.jpg]] | ||
Revision as of 08:26, 11 September 2008
Contents
1. Creating two DT signals (one periodic and one non-periodic) from a periodic CT signal
Let $ x(t) = sin (2\pi t), $ which is a periodic CT signal
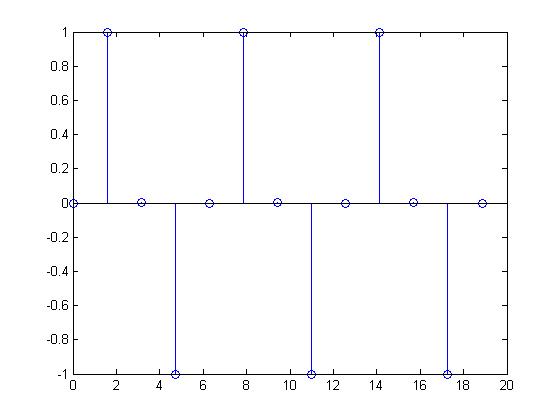
Periodic Signal
This discrete time signal was produced from a CT sine wave by sampling at a frequency of $ \frac{1}{\pi} $.
As can be seen from the graph, the values of x[n] are periodic because they repeat after every period of $ t = 2\pi $.
Therefore, $ x[n + 2\pi] = x[n] $
However, this still does not fulfill the requirement as $ N = 2\pi $ is not an integer. For the signal to become periodic, the CT waveform has to be modified to $ x(t) = sin(2\pi t) $ and sampled at a frequency of 1 Hz.
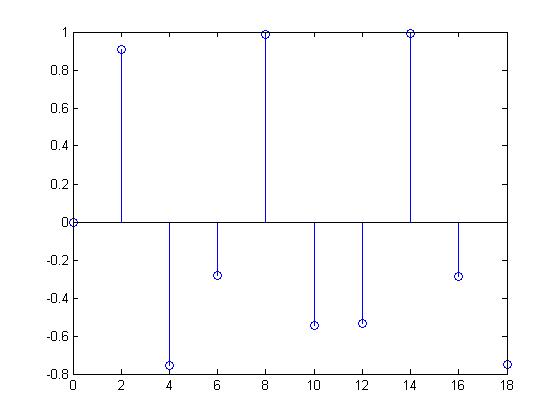
Non Periodic Signal
For this discrete time signal which was produced by sampling the same sine wave at a frequency of 0.5, the values of x[n] are non-periodic because the discrete time signal is scattered all over the place with no indication of a pattern. Therefore, $ x[n + k] \neq x[n] $