(→Part D: Time Invariance) |
(→Example of a Time-Invariant System) |
||
| Line 13: | Line 13: | ||
=== Example of a Time-Invariant System === | === Example of a Time-Invariant System === | ||
| + | |||
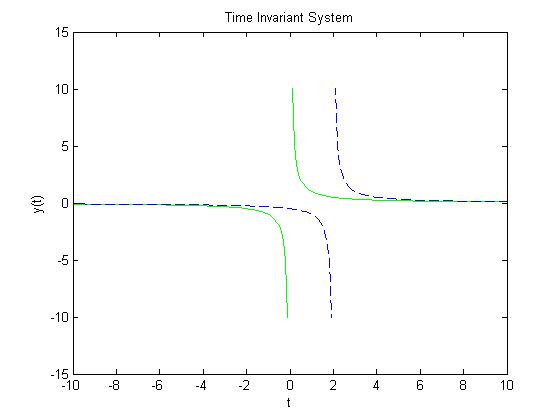
| + | An example of a time-invariant system is <math> y(t) = \frac{1}{t} </math>. | ||
| + | |||
| + | As you can see from the graph, <math> y</math><sub>2</sub><math>(t)</math> (the blue dotted graph) is the same graph of </math><sub>1</sub><math>(t)</math> (the green graph), but shifted to the right by <math>t</math><sub>0</sub><math>=2</math>. | ||
| + | [[Image:Untitled6_ECE301Fall2008mboutin.jpg]] | ||
Revision as of 15:19, 10 September 2008
Part D: Time Invariance
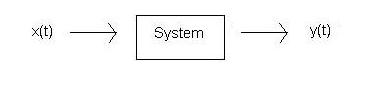
When a system is time invariant, any time shifting on the input signal will result in the same shifting of the output signal.
In other words (pictures),
implies
Example of a Time-Invariant System
An example of a time-invariant system is $ y(t) = \frac{1}{t} $.
As you can see from the graph, $ y $2$ (t) $ (the blue dotted graph) is the same graph of </math>1$ (t) $ (the green graph), but shifted to the right by $ t $0$ =2 $.