(→Creating a Periodic from a Non-Periodic Function) |
(→Creating a Periodic from a Non-Periodic Function) |
||
| Line 23: | Line 23: | ||
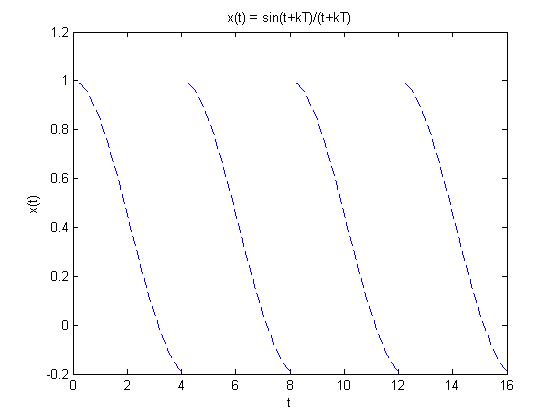
Using <math> x(t) = \frac{sin(t)}{t} </math>, which is a non-periodic function, we can create a periodic function by repeating the original function <math> x(t) </math> from <math> t = [0,4] </math> an infinite number of times. | Using <math> x(t) = \frac{sin(t)}{t} </math>, which is a non-periodic function, we can create a periodic function by repeating the original function <math> x(t) </math> from <math> t = [0,4] </math> an infinite number of times. | ||
| + | |||
| + | |||
| + | [[Image:Untitled4_ECE301Fall2008mboutin.jpg]] | ||
Latest revision as of 11:07, 10 September 2008
Contents
[hide]Part A: Periodic Signals Revisited
Periodic Continuous Time Signal
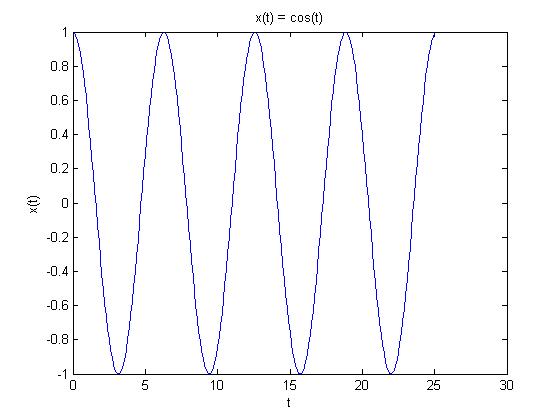
I used the continuous time signal $ x(t) = cos(t) $, as it seemed many people used in Homework 1 for their example of a periodic function. The signal repeats itself at intervals of $ 2\pi $.
Non-Periodic Discrete Time Signal
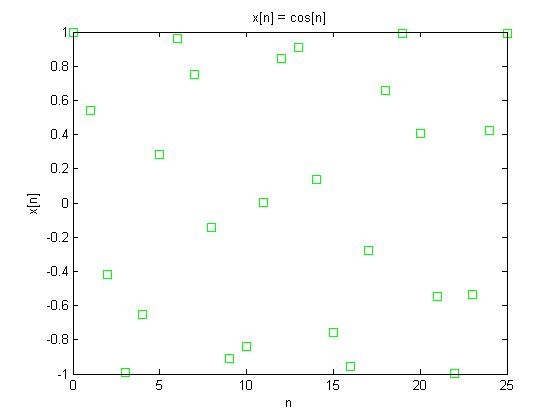
Using the CT signal $ x(t) = cos(t) $ and converting it to the DT signal $ x[n] = cos[n] $ will create a non-periodic function when n is sampled at every integer.
Periodic Discrete Time Signal
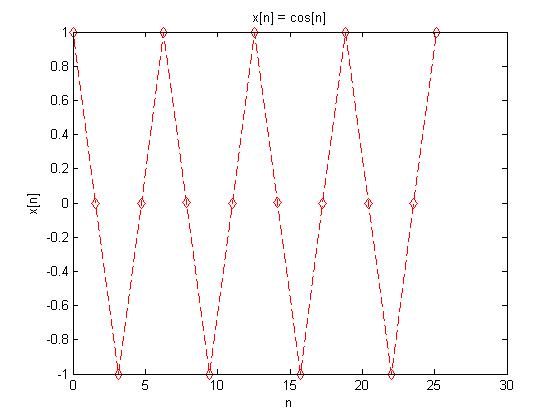
In order to create a discrete time signal $ x[n] = cos[n] $ that was still periodic, the time interval couldn't be integers, as shown previously. Therefore, a time interval of $ \pi/2 $ was selected.
Creating a Periodic from a Non-Periodic Function
Using $ x(t) = \frac{sin(t)}{t} $, which is a non-periodic function, we can create a periodic function by repeating the original function $ x(t) $ from $ t = [0,4] $ an infinite number of times.