(New page: == Continuous to discrete time signal== I used the signal <math>y = cos(n)\,</math> as the signal of my graph First lets look at sampling the graph at each 1 sec Image:hw2.1.jpg The...) |
(→Continuous to discrete time signal) |
||
| Line 15: | Line 15: | ||
As <math>y[n] = y[n+k], k = \R \,</math>, the function is periodic | As <math>y[n] = y[n+k], k = \R \,</math>, the function is periodic | ||
| + | |||
| + | == Creating periodic signals from no periodic signals == | ||
Revision as of 17:29, 9 September 2008
Continuous to discrete time signal
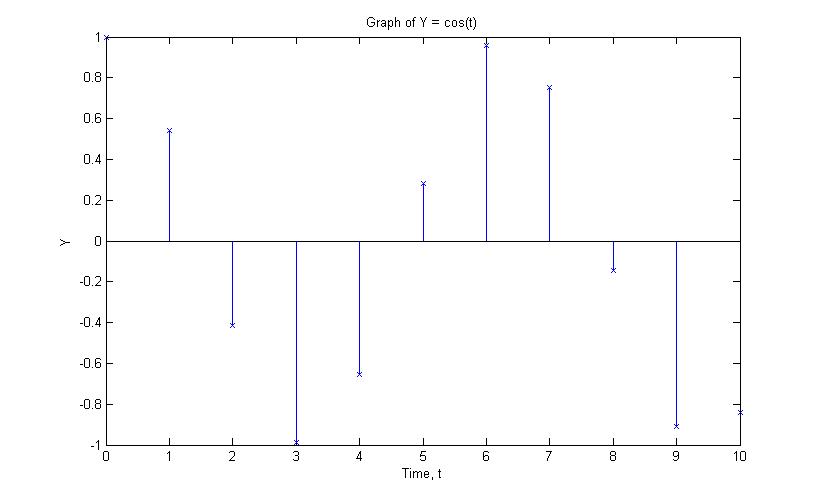
I used the signal $ y = cos(n)\, $ as the signal of my graph
First lets look at sampling the graph at each 1 sec
The dots are scattered everywhere, and is not periodic since $ y[n] \neq y[n+k], k \neq \R \, $
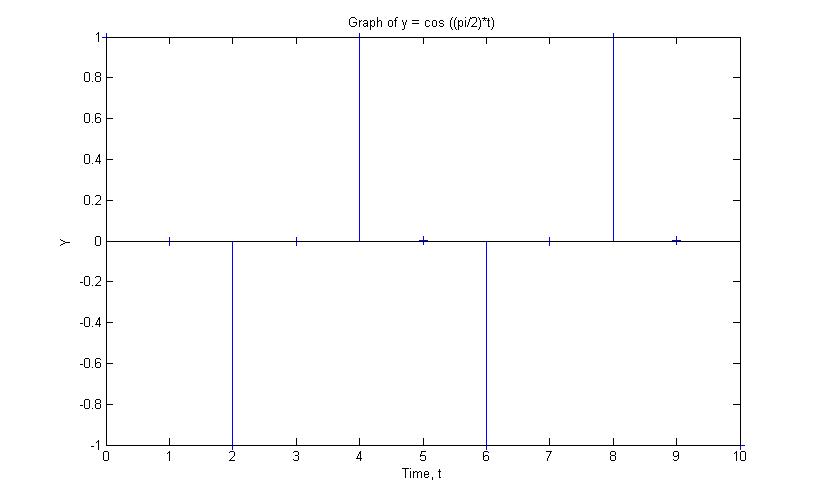
However, once we made some modifications to the graph, turn it into $ y = cos( \frac{\pi}{2} n)\, $, and sample it at every 1 sec
The dotes goes periodically from 1 to -1 and back to 1, every 4 seconds.
As $ y[n] = y[n+k], k = \R \, $, the function is periodic