(→Part A) |
(→Part A) |
||
| Line 6: | Line 6: | ||
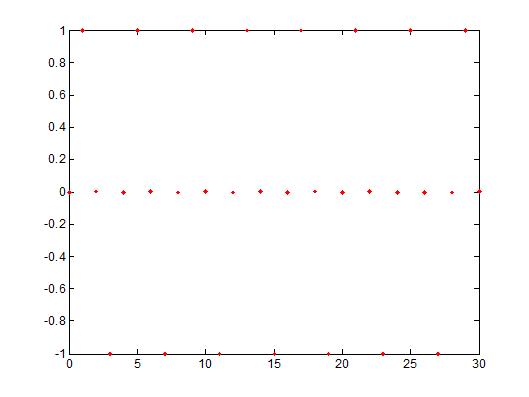
The plot on the left shows the same signal but in DT (y[n] = sin(n)). The sampling frequency is at <math>\pi/2</math> (y[n] = sin(<math>(\pi/2)</math>*n)). The signal repeats itself every 4 sec so that y[n] = y[n+4]. No = k * <math>\frac{2\pi}{\pi/2}</math> ==> No = k * 4 so that the signal repeats itself every 4 seconds. | The plot on the left shows the same signal but in DT (y[n] = sin(n)). The sampling frequency is at <math>\pi/2</math> (y[n] = sin(<math>(\pi/2)</math>*n)). The signal repeats itself every 4 sec so that y[n] = y[n+4]. No = k * <math>\frac{2\pi}{\pi/2}</math> ==> No = k * 4 so that the signal repeats itself every 4 seconds. | ||
| + | |||
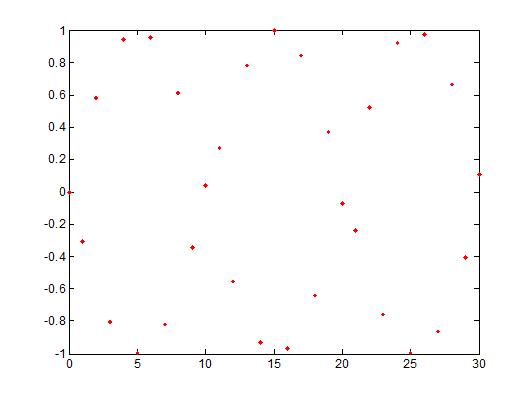
| + | The right picture is taken at a frequency of 10000 Hz so that y[n] = sin(10000 * n). As you can see the signal is not periodic because the value of No is not an integer. <math>No = k * \frac{2\pi}{10000} = \frac{\pi}{5000}</math> and this is not a rational integer. Therefore the signal in DT is not periodic. | ||
[[Image:sahw1a1_ECE301Fall2008mboutin.jpg]] [[Image:sahw1a3_ECE301Fall2008mboutin.jpg]] | [[Image:sahw1a1_ECE301Fall2008mboutin.jpg]] [[Image:sahw1a3_ECE301Fall2008mboutin.jpg]] | ||
Revision as of 17:07, 10 September 2008
Part A
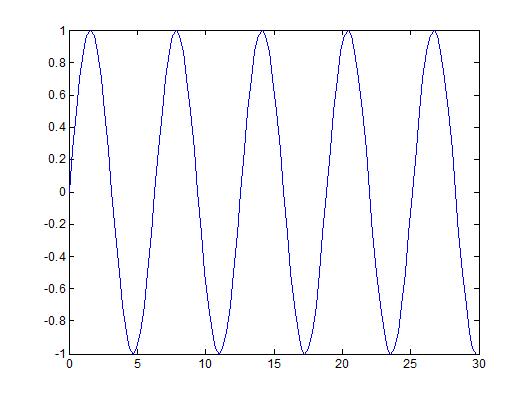
The original signal shown in the first plot is y(t) = sin(t) with a period of $ 2\pi $
The plot on the left shows the same signal but in DT (y[n] = sin(n)). The sampling frequency is at $ \pi/2 $ (y[n] = sin($ (\pi/2) $*n)). The signal repeats itself every 4 sec so that y[n] = y[n+4]. No = k * $ \frac{2\pi}{\pi/2} $ ==> No = k * 4 so that the signal repeats itself every 4 seconds.
The right picture is taken at a frequency of 10000 Hz so that y[n] = sin(10000 * n). As you can see the signal is not periodic because the value of No is not an integer. $ No = k * \frac{2\pi}{10000} = \frac{\pi}{5000} $ and this is not a rational integer. Therefore the signal in DT is not periodic.