Difference between revisions of "Swanson MA279 Fall2022 topic8" - Rhea

Revision as of 01:35, 24 November 2022

--Student33MA279F22 (talk) 17:18, 22 November 2022 (EST)

Introduction

Pi is possibly the most famous constant in mathematics. For thousands of years it has been a focus of mathematicians around the world. The earliest civilizations had a more limited understanding of mathematics than we have today but their rescillience lead to interesting solutions. Pi was originally held to be a rational number as there was no understanding of the possibility of irrational numbers. At a certain point it was discovered that its digits could extend forever and ways to calculate these digits became an area of discovery. There is a lot to consider throughout this history and even today. How many digits are necessary to know? Does the precision matter? Is there a best way to calculate the digits? Some questions relating to pi can be quite subjective but ultimately its objective value is of great importance to our understanding of the world and many physically practical applications.

Basic Approximations

Fundamentally, π is just the ratio between a circle's circumference and its diameter: c = πd. So you can estimate π by taking a circle, measuring it, and dividing the circumference by the diameter. One variation of this is to roll a wheel out on a road many times--the distance traveled by the wheel will be the circumference * the number of rotations taken by the wheel. The success of a pure measuring method will depend on the perfectness of your circle and the precision of your measuring tools.

Using rough approximation methods like this, some ancients initially thought that π = 22/7 (3.14285). However, it was later discovered that π is an irrational number, meaning it can't be represented by any fraction p/q where p and q are both integers. In order to determine π with a higher accuracy than simple measurement can achieve, mathematical calculation methods are needed.

- Bounds between 3 and 4 and how they are determined

Early Calculation

In some of the earliest historical records known of pi, it was recorded to be somewhere roughly between 3 and 4. Specifically, the Babylonians nearly 4,000 years ago seem to have believed pi was 25/8 or 3.125. The Egyptians (at around the same time) noted the pi was (16/9)^2 or roughly 3.16. The most well-known early algorithm for computing pi is popularly known from the mathematician Archimedes (and a similar, iterative method was used in China known as Liu Hiu's Pi Algorithm). Archimedes knew that pi was described as the ratio of a circle's circumference to its diameter and to him the most significant limiting factor in calculating pi was knowing the exact circumference of some theoretical circle defined by a known radius. He could however find a close approximation by creating polygons both inside and outside the circle with known side lengths to calculate pi. This grew ever closer to pi the more sides were added to these polygons but took a significant amount of work. There is a famous example of a man who dedicated decades to the calculation of pi using this method, his name was Ludolph van Ceulen. He calculated pi up to 35 places using this method and when he died the digits for his upper and lower bounds of pi (from the inner and outer polygons around the circle in the approximation) were inscribed on his tombstone.

Newtonian Calculation

Might want to find more references on this or use this video as the reference: https://www.youtube.com/watch?v=gMlf1ELvRzc Also might consider renaming this section "Infinite Series Calculation"

- Pascal's Triangle realization - Integration of unit circle - Infinite series and convergence rate optimization to find pi - Fun quote by Newton: "I am ashamed to tell you to how many figures I carried these computations, having no other business at the time."

Modern Calculation

- Algorithms by a computer - Reference the book Contact by Carl Sagan?

Today any computer or calculator can calculate the digits of pi, and there's even special-purpose software designed to calculate it exceptionally fast. Programs with names like QuickPi and PiFast compete to calculate the most digits of pi in the least amount of time.

Some people wonder how many digits of pi are currently known, but there isn't really an answer to this question, because thanks to the discovery of closed-form calculations, the answer is technically "all of them" (we can compute any given digit for you right now). The computation of a digit of pi without having to know preceding digits is referred to as digit extraction. The fastest formula currently known is Fabrice Bellard's, which can compute any digit of pi in O(n^2) time.

Interesting Calculation Methods

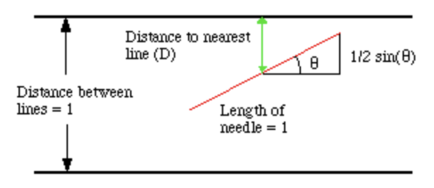
One interesting way to calculate π is by throwing a bunch of sticks on the ground, on a grid of parallel lines. By using the length of a stick, the size of the gaps between the lines, and the number of sticks that are crossing a line, we can find an estimate for π. This experiment is called Buffon’s needle, and you can try it for yourself here.

If we normalize the distance between lines to 1, we can draw each stick as follows, where D is the distance of its midpoint from the nearest line and θ is the angle of the stick from parallel. The needle will hit the line if D ≤ 1/2sin(θ).

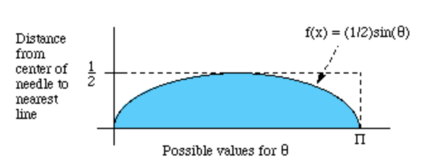
In order to determine how often this happens, we can plot 1/2sin(θ) on a graph. As you can see, D can range from 0 to ½ and θ can range from 0 to π radians. The blue area of the graph is where D ≤ 1/2sin(θ). So in order to find the probability that D ≤ 1/2sin(θ), we can take the area of the blue curve divided by the area of the rectangle of total possibilities.

The area under the blue curve, found using integration, is 1, and the area of the enclosing rectangle is π/2. So (needles touching a line)/(total needles) ≈ 1/(π/2) = 2/π. We can input our real data and rearrange this equation to approximate pi. This kind of calculation isn't very practical, but if you get too frustrated with infinite series and calculus then we've found throwing sticks on the ground to be quite cathartic.

Applications

Knowing pi is valuable any time you want to calculate the volume or surface area of a cylinder or sphere. For example, a water bottle manufacturer who wants to know how much metal they need to make a water bottle with specified dimensions can use pi to calculate the volume of the bottle. They could also use it to find the surface area of the bottle, to determine how much paint they need to color it. In a similar vein, a construction company might use pi to figure out how much concrete they need for a circular pillar.

Another use-case for pi is related to circular velocity--for example, determining how fast a piston connected to the wheels on a train is moving.

In practice, most applications of pi require no more than a few digits of precision, and even things like the calculation of orbits and trajectories for interplanetary navigation need no more than dozens of digits. People have calculated trillions of digits of pi not for any particular use but just because they can.

- Drink containers? - Super computing benchmarks? - Car tires? - Others?

References

- Likely clean these up to look more APA

https://en.wikipedia.org/wiki/Pi https://en.wikipedia.org/wiki/Approximations_of_π - might need to use this more heavily https://en.wikipedia.org/wiki/Liu_Hui%27s_π_algorithm https://en.wikipedia.org/wiki/Chronology_of_computation_of_π - unused currently, might be a useful graphic https://mathshistory.st-andrews.ac.uk/Biographies/Van_Ceulen/ https://www.universetoday.com/110331/happy-pi-day-5-ways-nasa-uses-pi/#:~:text=In%20basic%20mathematics%2C%20Pi%20is,flight%2C%20to%20name%20a%20few. - unused currently, might be useful https://mste.illinois.edu/activity/buffon/ https://ogden.eu/pi/ https://en.wikipedia.org/wiki/Approximations_of_%CF%80#Digit_extraction_methods