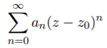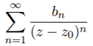| Line 45: | Line 45: | ||
<br /> | <br /> | ||
<gallery> | <gallery> | ||
| − | File:Residue1.png | + | File:Residue1.png |
</gallery> | </gallery> | ||
In this expanded form, h-1 is the residue of h(z) at z0, which we can write as Res┬(z→z0)〖h(z)〗. | In this expanded form, h-1 is the residue of h(z) at z0, which we can write as Res┬(z→z0)〖h(z)〗. | ||
| Line 55: | Line 55: | ||
<br /> | <br /> | ||
<gallery> | <gallery> | ||
| − | File:Laurent1.png | + | File:Laurent1.png |
</gallery> | </gallery> | ||
We call this the “Laurent Series for f around z0. On the right side of the addition operator we have: | We call this the “Laurent Series for f around z0. On the right side of the addition operator we have: | ||
<br /> | <br /> | ||
<gallery> | <gallery> | ||
| − | File:Laurent2.png | + | File:Laurent2.png |
</gallery> | </gallery> | ||
We call this the analytic/regular part of the Laurent Series. On the left side of the addition operator we have: | We call this the analytic/regular part of the Laurent Series. On the left side of the addition operator we have: | ||
<br /> | <br /> | ||
| − | + | <gallery> | |
| + | File:Laurent3.png | ||
| + | </gallery> | ||
This is called the singular/principle part of the Laurent Series. This principle part is important, because when z0 is plugged into the function f(z), the principle part causes f(z0) to be undefined. This means the Laurent Series can expand around a point where the function isn’t defined, or its singularity. | This is called the singular/principle part of the Laurent Series. This principle part is important, because when z0 is plugged into the function f(z), the principle part causes f(z0) to be undefined. This means the Laurent Series can expand around a point where the function isn’t defined, or its singularity. | ||
<br /> | <br /> | ||
Revision as of 13:54, 6 December 2020
Contents
Cauchy’s Residue Theorem
Oscar Su | Data Science Major
The Residue Theorem is an important theorem in the field of Complex Analysis. It will require an understanding of many concepts not yet learned by most Multivariable Calculus students. To help with the learning process, brief introductions of the elementary topics in Complex Analysis will be provided to act as building blocks for learning Cauchy’s Residue Theorem. Table of Contents
- Complex Analysis
- Cauchy’s Integral Theorem
- Residue
- Laurent Series
- Cauchy’s Residue Theorem (Main Discussion)
- References
Complex Analysis
Complex Analysis is a branch of Mathematical Analysis that deals with the study of complex numbers, as well as their functions and derivatives. Applications of Complex Analysis can be mostly be found in quantum mechanics, aerospace engineering, and mechanical engineering.
A complex number is defined as any number that can be written as a + bi where a and b represent real numbers with i being the imaginary unit. In this form, a would be considered the real part, while b would be considered the imaginary part.
A function f is said to be complex differentiable if lim┬(h→0)〖(f(z+h) - f(z))/h〗 exists provided f takes in a complex number and returns one as well. If f remains complex differentiable while z takes on the value of any complex number, f is said to be holomorphic.
This notably is similar to the definition for differentiability of a real function. However, there are a few key distinctions between the two. The complex differentiability condition has a much “stronger” implication than real function differentiability.
If a function is considered holomorphic, it is also infinitely differentiable. This means the existence of the nth derivative implies the existence of the (n+1)th derivative, as well as all subsequent derivatives. Real functions on the other hand are not infinitely differentiable. Holomorphic functions will always satisfy all the properties of analytical functions, whereas real functions do not.
An analytical function is a function that is locally given by a convergent power series at every point in its domain. This means they are continuous and differentiable everywhere. Almost all functions we can obtain from basic algebraic operations are analytic.
Cauchy’s Integral Theorem
The Integral Theorem is used in:
Assume we have a function f(z) with C being a closed curve. In order to use the theorem, three conditions must be satisfied:
- f(z) is holomorphic over all points on and in C.
- C is a simple closed curve.
- C has a finite number of corners.
If all conditions are true, then we may use the Integral Theorem to conclude ∮_C▒〖f(z)dz=0〗. Simply put, if f is holomorphic, then its contour integral along a simple closed curve will be 0.
Residue
In Complex Analysis, residue refers to complex number that is proportional to a contour integral over a path around a pole of a meromorphic function. A contour integral is simply a line integral in a complex plane.
A function is considered meromorphic if it is holomorphic on all points in an open subset with the exception of a set of isolated points, called the poles of the function. At those poles, the function is considered singular. An open set is an interval on a real line exclusive of its endpoints. They can also be thought of as complex functions expressed as the ratio of two analytic functions. If we have two functions f(z) and g(z) which are analytic at z0 and a function h(z) which is represented by (f(z))/(g(z)), then h(z) is meromorphic at z0. We can expand h(z) into:
In this expanded form, h-1 is the residue of h(z) at z0, which we can write as Res┬(z→z0)〖h(z)〗.
Laurent Series
We can begin by thinking of Laurent Theorem as the Taylor Theorem of complex functions instead of real functions. To set this up, imagine two concentric circles on the complex plane, with one being greater in size than the other. We name R as the region between the two. The shared center of both circles is a point called z0. Let’s say we have a function f(z) which is holomorphic in R. Using Laurent’s Theorem, we can expand f(z) into the Laurent Series below.
We call this the “Laurent Series for f around z0. On the right side of the addition operator we have:
We call this the analytic/regular part of the Laurent Series. On the left side of the addition operator we have:
This is called the singular/principle part of the Laurent Series. This principle part is important, because when z0 is plugged into the function f(z), the principle part causes f(z0) to be undefined. This means the Laurent Series can expand around a point where the function isn’t defined, or its singularity.
To find the coefficients of the Laurent Series, we must use contour integrals. To find the coefficient of the analytic part, we use this integral:
To find the coefficient of the principle part, we use this integral:
Cauchy’s Residue Theorem (Main Discussion)
The Residue Theorem is used to evaluate line integrals of analytic functions over closed curves.
Let’s suppose that f(z) is a complex analytical function with a set of isolated singularity points. Curve C is a simple closed curve that is positively oriented (counterclockwise). In this example z1, z2, and z3 are singularities.
According to the Residue Theorem, the contour integral for f(z) will be 2πi multiplied with the sum of the residues of f at each of the singularities.
References
https://www.youtube.com/watch?v=6KYWv2bfAc4&ab_channel=Fematika https://brilliant.org/wiki/holomorphic-function/ http://ksacg.faculty.ku.edu/ksacg/145/2016_Fall/Math_symbols%20.pdf https://en.wikipedia.org/wiki/Complex_analysis https://en.wikipedia.org/wiki/Analytic_function https://byjus.com/maths/analytic-function/ https://math.stackexchange.com/questions/1400997/what-is-a-residue https://math.wikia.org/wiki/Residue https://mathworld.wolfram.com/ContourIntegral.html https://mathworld.wolfram.com/MeromorphicFunction.html https://www.youtube.com/watch?v=YE7PogQr7Os&ab_channel=GraduateMathematics https://www.youtube.com/watch?v=0ZOMkmy-aTo&ab_channel=FacultyofKhan https://math.mit.edu/~jorloff/18.04/notes/topic4.pdf https://www.youtube.com/watch?v=qTDDFMAt7j4&ab_channel=FacultyofKhan https://math.mit.edu/~jorloff/18.04/notes/topic7.pdf https://en.wikipedia.org/wiki/Residue_theorem https://www.youtube.com/watch?v=YWIseo5LwgQ&ab_channel=FacultyofKhan https://math.mit.edu/~jorloff/18.04/notes/topic8.pdf