Difference between revisions of "Walther MA279 Fall2018 topic9" - Rhea

Revision as of 20:48, 2 December 2018

Xinping Zhang, Albert Xu, Ji Ma, Alicia Troyer, Ryan Sullivan
Uli Walther
MA 279 Great Issues in Mathematics
15 November 2018

Malthus Doctrine

Introduction

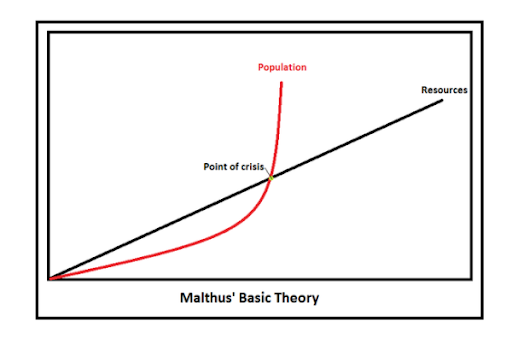
The Malthus Doctrine, or Malthus Theory of Population Growth, was first introduced in a 1798 publication titled An Essay on the Principle of Population. It was developed by Thomas Robert Malthus, an English scholar. Malthus’s doctrine discusses population growth, food supply, and the events that occur when population reaches a number past that which can be naturally sustained. He claimed that rapid population growth is dangerous because the supply of food and other resources grows at a much slower rate, causing population growth to become unsustainable. However, Malthus also claimed that there are ways to prevent unsustainability, which include both actions individuals could take and events that occur naturally to decrease population sizes to a sustainable level (Pepper). Though parts of his theory could still prove to be true, over the years there have been many criticisms of the Malthusian Doctrine because of his lack of accounting for several elements (Tushar).

The Malthus Doctrine has two main components. First, the doctrine states that population, when left unchecked, increases exponentially due to human nature (Malthus 4). The second component says that food supply can only increase linearly. Given enough time, an exponential sequence will always surpass a linear sequence. In fact, the ratio of an exponential sequence and a linear sequence has no upper bound as ngrows. Due to these components, Malthus made the prediction that population growth would surpass the growth rate of food production resulting in a calamity unless actions were taken. Malthus recognized two types of controls that prevent human population from growing indefinitely. The first type is a positive check, which includes things such as war, mass starvation, and disease. When population greatly exceeds food supply, these checks trigger and bring population back to a sustainable level. The second type of check Malthus identified is a preventive check. Preventive checks are measures taken that reduce the birth rate causing population growth to slow (Tushar). Delaying marriage and limiting birth rates are examples of preventative measures that could be used to control population growth. Malthus deduced that if no preventive checks are in place, the world naturally becomes overpopulated, and positive checks begin to take effect.

Malthus’ Theory of Population has limited applicability to modern society. The theory has been criticized and deconstructed in several ways. One such aspect is population growth is not purely exponential. Adolphe Quetelet, a statistician, noted in 1835 that population cannot grow exponentially for a long time (Bacaër 35). Later, in 1838, Verhulst published his Note on the law of population growth. In that paper, Verhulst pointed out that Malthus Theory ignores the increasing difficulty of maintaining a large population. Verhulst claimed that as population becomes larger, growth slows down due to resource limitations. The environment has a finite amount of resources, and the amount of resource determines the maximum population the environment can support. This upper limit is often referred to as “carrying capacity.” When population size is relatively low, it can grow exponentially, in accordance with the Malthus Doctrine. However, as population approaches the environment’s carrying capacity, growth tends to slow down. The population might stabilize at a fixed point near the carrying capacity, or it might go above the capacity. In the second case, positive checks will cause population to decline until it falls below the carrying capacity.

There is significant evidence to support Verhulst’s claims about population growth. According to world bank's data, world’s population over the last 57 years showed linear growth with R2=0.9986. This supports the idea that population growth is not entirely exponential. Verhulst, a French mathematician, checked population census data in France, Belgium, Russia, Essex, and England in the early 19th century and proposed the following equation for population growth to accommodate concerns addressed above (Seidl 398):

$ \frac{dN}{dt}=rN(\frac{K-N}{K}) $

where Nis the population size, Kis the carrying capacity, and ris a growth rate. The growth rate is a parameter that is likely to differ from one population group to another. This equation captures all points stated before. When Nis small relative to K, K-NKis nearly 1, which means growth rate is about rN. As Ngrows towards K, K-NKapproaches 0. When N=K, K-NK=0, and population growth is completely halted. If Ngrows above K, K-NKwould be negative meaning the population would be declining. This makes sense because if the population is greater than the carrying capacity, there would not be enough resources to sustain such a population, and it would therefore decline. The greater Nis the faster the decline. Verhulst’s equation is called the logistic equation, or logistic growth model. It is a better population growth model than Malthus’s purely exponential model.

Modern high tech solutions have greatly increased the rate of growth of the world’s food supply, contradicting Malthus’ belief that the food supply grows linearly over time. Throughout history, humanity has found clever solutions to fight food shortage. For example, in the 1940’s people were starving because pests and disease were decimating produce around the world. Scientists were soughts a solutions, and eventually responded to the famine with the discovery of DDT (dichloro-diphenyl-trichloroethane). DDT was the first synthetic insecticide to improve large scale crop production. It utilizes advanced chemical technology to control pest populations and to prevent them from destroying crops. According to R. Yeadon, DDT residues in soil and crops were calculated by GLC analysis at the end of each growing season and showed disappearance of at least 60 percent of the applied pesticide. Though DDT is now identified as a very lethal chemical, and is forbidden for any crop production, it did help the population in 1940s to overcome the starving issue.

There are even more modern examples of how technology is used to produce more food with less resources. A group of futuristic foods are gradually impacting our daily life. One popular food replacement project, Soylent, which was kickstarted by a group of entrepreneurs in silicon valley, has created a promising meal replacement drink. The beverage consists of extracted nutrients such as fats, proteins, vitamins, and carbohydrates from plants as well as other easily accessible food sources. The CEO of soylent stated that this three dollar meal replacement satisfies all of a person’s daily required nutrients. By reducing the cost of the food production, this high tech meal replacement consisting of alternative nutrient sources could drastically increase the carrying capacity of the environment, and increase the quality of life for the current population of the world. Because of all of these technological advancements, today in the majority of developed countries, instead of population growth being higher than food production as predicted by Malthus, the opposite has occurred. This means many developed countries today are actually producing food at a more rapid pace than the population growth rate in that country (Tushar).
Another criticism of the Malthusian Theory is that he failed to account for the role that other types of production played when it came to supporting a sizeable population with food. When making the prediction about the growth rate of food being arithmetic, Malthus used the basis that land was a limited resource. In his belief, this meant that the growth rate of food was much more limited than population growth which would inevitably result in a crisis. This did not come to pass however, because as countries such as England began to enter the Industrial Revolution, they began to focus on and use other natural and man-made resources (Tushar). This allowed people to shift total concentration from food production and led to global trade. Trade allows places with large populations to acquire food from others in the event that they do not have the resources and land to grow their own. Because of this, food has become more available to society than Malthus once predicted (Agarwal). There is some belief that Malthus overlooked this fact due to his attention being mainly focused on England and the problems faced there at the time. In this time period for example places such as the United States and Argentina were just starting to produce substantial amounts of food (Zafar).

Modern Malthusianism focuses on ecological factors in addition to the food supply. With the increase in ecological research and the advent of concern over global warming, some are starting to worry that factors aside from food production will limit the Earth’s carrying capacity. This wave of neo-Malthusianism contends that due to a combination of pollution and food scarcity, the Earth will eventually reach a population crisis (Howard 2005). While these people still believe that unbounded population growth is exponential, they recognize that growth is often bounded by limited resources. Many also now believe that due to advances in technology, food production grows faster than a simple linear model.
The original Malthus Doctrine had many significant flaws, but the primary concepts are still important to modern discourse. Although Malthus’ original description of exponential population growth and linear food growth has been contested, it still serves as a crude description of the problems facing growing populations. This is evident from the many derivative concepts that his work spawned, such as the logistic growth model, and neo-Malthusianism. In total, Malthus defined a framework for understanding the nature of population growth which still motivates and inspires discussion of the subject over 200 years later.

"References"
Agarwal, Prateek. “Malthusian Theory of Population.” Intelligent Economist.Intelligent Economist, 2018, https://www.intelligenteconomist.com/malthusian-theory/. Accessed 29 November 2018.
Pepper, David. “Malthusian Doctrine.” Environmental Geology.(1999 ed.) Kluwer Academic Publishers, 1999, https://link.springer.com/referenceworkentry/10.1007%2F1-4020-4494-1_213. Accessed 26 November 2018.
Tushar, Seth. “Malthusian Theory of Population: Explained with its Criticism.” Economics Discussion.http://www.economicsdiscussion.net/articles/malthusian-theory-of-population-explained-with-its-criticism/1521. Accessed 27 November 2018.
Zafar, Sultan. “Malthusian Theory of Population: Criticisms and Applicability.” Linkedin.Linkedin, 2016, https://www.linkedin.com/pulse/malthusian-theory-population-criticisms-applicability-sultan-zafar. Accessed 29 November 2018.
Kunstler, James Howard. The Long Emergency. 2006, www.fnac.com/livre-numerique/a12825138/James-Howard-Kunstler-The-Long-Emergency. Accessed 2 Dec. 2018.