| Line 36: | Line 36: | ||
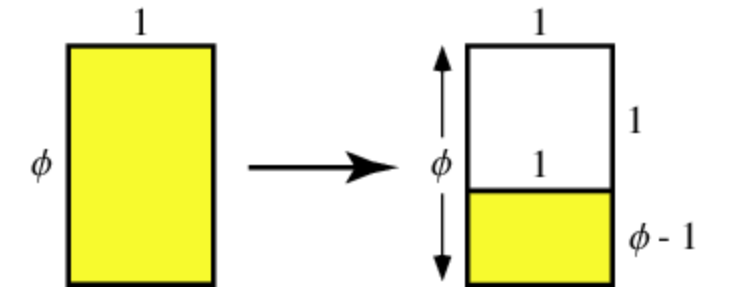
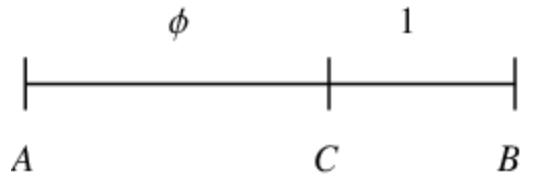
Visualizations of the golden ratio can be seen below (Weisstein): | Visualizations of the golden ratio can be seen below (Weisstein): | ||
| − | <center>[[File:Visualization 1.png| | + | <center>[[File:Visualization 1.png|none]] </center> |
<center>[[File:Visualization 2.png|framed]] </center> | <center>[[File:Visualization 2.png|framed]] </center> | ||
[https://www.mathsisfun.com/numbers/golden-ratio.html MathIsFun] also has an interactive display that can construct a rectangle in the golden ratio given a certain fixed width or length. | [https://www.mathsisfun.com/numbers/golden-ratio.html MathIsFun] also has an interactive display that can construct a rectangle in the golden ratio given a certain fixed width or length. | ||
Revision as of 16:35, 2 December 2018
Introduction
The golden ratio is a ratio such that, given two quantities a and b,
We can solve this equation to find an explicit quantity for the ratio.
We set the ratio equal to a certain quantity given by r.
Then we can solve for the ratio numerically.
We can see from the above result that the golden ratio can also be described as a ratio such that in order to get the square of the ratio, you add one to the ratio.
We can then apply the quadratic formula to solve for the roots of the equation.
The positive root is then the golden ratio.
The golden ratio, $ \phi $, is sometimes also called the golden mean or the golden section. The golden ratio can be frequently observed in man-made objects, though they are generally “imperfectly golden” – that is, the ratio is approximately the golden ratio, but not exactly. Some everyday examples include: credit cards, $ \frac{w}{h}=1.604 $, and laptop screens, $ \frac{w}{h}=1.602 $ (Tannenbaum 392).
Visualizations of the golden ratio can be seen below (Weisstein):
MathIsFun also has an interactive display that can construct a rectangle in the golden ratio given a certain fixed width or length.