| Line 10: | Line 10: | ||
The golden angle is simply the golden ratio applied to a circle: it is the smaller angle formed by two arcs that are related by the golden ratio. | The golden angle is simply the golden ratio applied to a circle: it is the smaller angle formed by two arcs that are related by the golden ratio. | ||
<center> <math> \frac{a}{b} = \frac{a+b}{a} = \frac{360^o}{\theta} = \frac{1}{\phi} </math> </center> | <center> <math> \frac{a}{b} = \frac{a+b}{a} = \frac{360^o}{\theta} = \frac{1}{\phi} </math> </center> | ||
| − | <center> <math> \theta = \phi | + | <center> <math> \theta = \phi \cdot 360^o \approx 137.5^o </math> </center> |
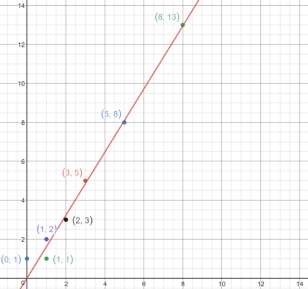
This angle minimizes the amount of overlap between the layers of leaves, maximizing the amount of sunlight the plan can receive. One method of seeing why this is the case is to consider the graph <math> y = \frac{1}{\phi} x </math>, plotted in Figure 3. | This angle minimizes the amount of overlap between the layers of leaves, maximizing the amount of sunlight the plan can receive. One method of seeing why this is the case is to consider the graph <math> y = \frac{1}{\phi} x </math>, plotted in Figure 3. | ||
Revision as of 19:17, 1 December 2018
The Fibonacci Sequence in Leaves
The Fibonacci sequence is present in both the structure and arrangement of leaves in many plants. Since plants rely on photosynthesis, they want to maximize the amount of sunlight that strikes their leaves. The vertical growth of many plants means that leaves can cover up each other. To minimize this effect, the leaves are grown such that the angle between each successive leaf is the golden angle, as shown in Figure 2.

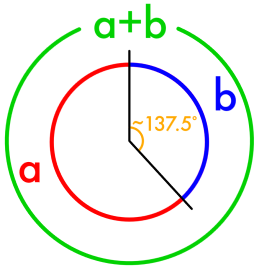
The golden angle is simply the golden ratio applied to a circle: it is the smaller angle formed by two arcs that are related by the golden ratio.
This angle minimizes the amount of overlap between the layers of leaves, maximizing the amount of sunlight the plan can receive. One method of seeing why this is the case is to consider the graph $ y = \frac{1}{\phi} x $, plotted in Figure 3.