| Line 13: | Line 13: | ||
The Fibonacci sequence cannot be discussed independently of the golden ratio. The golden ratio, denoted by φ, is equal to: | The Fibonacci sequence cannot be discussed independently of the golden ratio. The golden ratio, denoted by φ, is equal to: | ||
<center> <math> φ = \frac{1 + \sqrt{5}}{2} \approx 1.618 ... </math> </center> | <center> <math> φ = \frac{1 + \sqrt{5}}{2} \approx 1.618 ... </math> </center> | ||
| + | |||
| + | The value of the golden ratio can be found using a variety of method. For example, consider the golden rectangle seen below. | ||
| + | <center> https://www.miniwebtool.com/s/i/golden-rectangle.png </center> | ||
| + | <center> Figure 2: The Golden Rectangle </center> | ||
| + | A golden rectangle is constructed by taking a square of side length a, and extending it a length b so that the following is true: | ||
| + | <center> <math> \frac{a}{b} = \frac{a + b}{a} </math> </center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
Revision as of 15:42, 28 November 2018
Introduction
The Fibonacci sequence is one of the more widely known integer sequences used in mathematics. An integer sequence is simply an ordered list of integers (0, ±1, ±2, …). The Fibonacci sequence is typically constructed recursively; the nth term of the sequence can be determined by the previous terms. Beginning with 0 and 1, the Fibonacci sequence is given by:
that is to say that the nth term is the sum of the previous two terms of the sequence. The first several Fibonacci numbers are then:
At first glance, the Fibonacci sequence seems relatively benign. However, it is related to many phenomena observed in nature, due to how the sequence can be represented graphically. Consider the rectangle in Figure 1. It has been constructed by combining squares with side lengths equal to the Fibonacci numbers in a cyclical manner. A spiral can be created by drawing a portion of a circle within each square. The result is the Fibonacci spiral, which appears in many plant structures. Specifically, the Fibonacci sequence is prominent in the phyllotaxis, or leaf arrangement, of plants.

The Fibonacci sequence cannot be discussed independently of the golden ratio. The golden ratio, denoted by φ, is equal to:
The value of the golden ratio can be found using a variety of method. For example, consider the golden rectangle seen below.
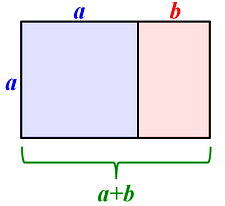
A golden rectangle is constructed by taking a square of side length a, and extending it a length b so that the following is true:

