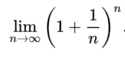| Line 1: | Line 1: | ||
| − | '''<big>The Mysteries of the number ''e''</big>''' | + | == '''<big>The Mysteries of the number ''e''</big>''' == |
| − | The number "e" is one of the most important constants in all of mathematics. The value of "e" is approximately 2.71828... and goes on infinitely as it is irrational. Jacob Bernoulli originally came up with a formula for the constant in 1683 while he was doing work related to compound interest. However, it was Leonard Euler in 1731 who did a lot of work with the number and ended up giving it the symbol "e" as it is known today. Since then the number has played an important role in a number of fields | + | '''Introduction'''<br /> |
| + | |||
| + | The number "e" is one of the most important constants in all of mathematics. The value of "e" is approximately 2.71828... and goes on infinitely as it is irrational. Jacob Bernoulli originally came up with a formula for the constant in 1683 while he was doing work related to compound interest. However, it was Leonard Euler in 1731 who did a lot of work with the number and ended up giving it the symbol "e" as it is known today. Since then the number has played an important role in a number of fields past just mathematics including finance and physics. | ||
| + | |||
| + | '''Defining ''e''''' <br /> | ||
| + | |||
| + | When Jacob Bernoulli was studying compound interest in 1683, he came up with a formula he was trying to find a value for:<br /> | ||
| + | [[File:Bernoulli.png|125px|thumbnail|Bernoulli's Formula]]. If one were to use bigger and bigger values of ''n'', the result would eventually | ||
Revision as of 22:13, 26 November 2018
The Mysteries of the number e
Introduction
The number "e" is one of the most important constants in all of mathematics. The value of "e" is approximately 2.71828... and goes on infinitely as it is irrational. Jacob Bernoulli originally came up with a formula for the constant in 1683 while he was doing work related to compound interest. However, it was Leonard Euler in 1731 who did a lot of work with the number and ended up giving it the symbol "e" as it is known today. Since then the number has played an important role in a number of fields past just mathematics including finance and physics.
Defining e
When Jacob Bernoulli was studying compound interest in 1683, he came up with a formula he was trying to find a value for: