(Created page with "'''Sampling theorem-''' ''As long as a signal is both band-limited and the period is small enough then the signal can be recovered using Xd[n]]X(nT).'' '''Questions y...") |
|||
| Line 42: | Line 42: | ||
| Rec (Frequency Domain)|| Ex: X(w)=u(w)-u(w-1) | | Rec (Frequency Domain)|| Ex: X(w)=u(w)-u(w-1) | ||
|- | |- | ||
| − | | Modulation 1 (Exponential Carrier)||[[File:exponential_carrier. | + | | Modulation 1 (Exponential Carrier)||[[File:exponential_carrier.png|thumbnail]] |
|- | |- | ||
| − | | Demodulation 1 (Exponential Carrier)||[[File:exponential_carrier1. | + | | Demodulation 1 (Exponential Carrier)||[[File:exponential_carrier1.png|thumbnail]] |
|- | |- | ||
| − | | Modulation 2 (Sine Carrier)||[[File:sine_carrier. | + | | Modulation 2 (Sine Carrier)||[[File:sine_carrier.png|thumbnail]] |
|- | |- | ||
| − | | Demodulation 2 (Sine Carrier)||[[File:sine_carrier1. | + | | Demodulation 2 (Sine Carrier)||[[File:sine_carrier1.png|thumbnail]] |
|- | |- | ||
| − | | Modulation 3(Impulse Train Carrier) ||[[File:impulse_train_carrier. | + | | Modulation 3(Impulse Train Carrier) ||[[File:impulse_train_carrier.png|thumbnail]] |
|- | |- | ||
| − | | Demodulation 3 (Impulse Train Carrier)||[[File:impulse_train1. | + | | Demodulation 3 (Impulse Train Carrier)||[[File:impulse_train1.png|thumbnail]] |
|} | |} | ||
Latest revision as of 02:22, 23 November 2018
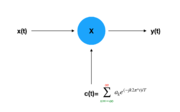
Sampling theorem- As long as a signal is both band-limited and the period is small enough then the signal can be recovered using Xd[n]]X(nT).
Questions you should ask yourself when tackling these problems:
- Is the signal band-limited?
- What is the nyquist rate? (2wm)
- Does it meet the nyquist condition?(ws>2wm)
- If the nyquist condition is not met, does the signal overlap?
Things you keep in mind when tackling these problems:
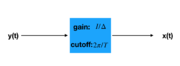
- If a signal does not meet the nyquist condition but the impulse train does not overlap then the signal can still be recovered by applying a filter.
- A rec in the time domain is equivalent to a sinc in the frequency domain.
- A sinc in the time domain is equivalent to a rec in the frequency domain.
- Time shifting (Ex: $ x(t-t_0) \ $->$ e^{-j\omega t_0}X(\omega) $ ) does not affect the nyquist rate.
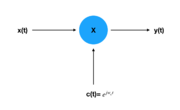
- Frequency shifting (Ex: $ e^{j\omega_0 t}x(t) $ -> $ \mathcal{X} (\omega - \omega_0) $) affects the nyquist rate.
| Random Useful stuff | stuff |
| CTFT Properties | CTFT |
| Nyquist Rate | 2wm |
| Sampling Rate | ws=$ 2pi/T $ |
| Nyquist Condition | ws>2wm |
| Sinc (Time Domain) | Ex: x(t)=$ sin(wt)/t $ |
| Sinc (Frequency Domain) | Ex: X(w)=$ sin(wt)/w $ |
| Rec (Time Domain) | Ex: x(t)=u(t)-u(t-1) |
| Rec (Frequency Domain) | Ex: X(w)=u(w)-u(w-1) |
| Modulation 1 (Exponential Carrier) | |
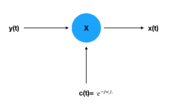
| Demodulation 1 (Exponential Carrier) | |
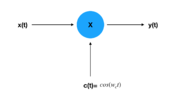
| Modulation 2 (Sine Carrier) | |
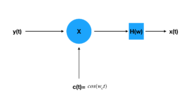
| Demodulation 2 (Sine Carrier) | |
| Modulation 3(Impulse Train Carrier) | |
| Demodulation 3 (Impulse Train Carrier) |