| Line 10: | Line 10: | ||
X(<math>\omega</math>) = 0 for <math>|\omega|>\omega_m</math> | X(<math>\omega</math>) = 0 for <math>|\omega|>\omega_m</math> | ||
| − | 3. <math> 2\pi/T = \omega_s > 2\omega_m</math> | + | 3. <math> 2\pi/T = \omega_s > 2\omega_m</math> (Nyquist Condition) |
Then x(t) is uniquely recoverable. | Then x(t) is uniquely recoverable. | ||
Latest revision as of 14:13, 30 April 2018
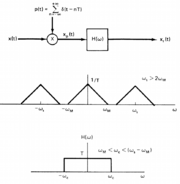
Explanation of Sampling Theorem
The sampling theorem:
1. for x(nT) to be equally spaced samples of x(t), while n=0, +1, -1, +2, -2, ...
2. x(t) is band limited. X($ \omega $) = 0 for $ |\omega|>\omega_m $
3. $ 2\pi/T = \omega_s > 2\omega_m $ (Nyquist Condition)
Then x(t) is uniquely recoverable.
Here is a block diagram of sampling and reconstruction using a LPF: