| Line 6: | Line 6: | ||
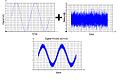
When there are only 1 non-zero term, the time and frequency domain are shown below: | When there are only 1 non-zero term, the time and frequency domain are shown below: | ||
| − | |||
<gallery> | <gallery> | ||
| − | File: | + | File:Example.jpg|Caption1 |
| + | File:Example.jpg|Caption2 | ||
</gallery> | </gallery> | ||
When 2 non-zero terms | When 2 non-zero terms | ||
Revision as of 14:51, 21 April 2018
Approximating Periodic Signals with Finite Fourier Series
In this project, a matlab function will be used to show how a finite number of Fourier Series coefficients can approximate a periodic signal.
When there are only 1 non-zero term, the time and frequency domain are shown below:
When 2 non-zero terms
When 5 non-zeros terms
When there are 25 non-zero terms
Conclusion: From the above diagrams we are able to distinguish that: As the number of Fourier Series Coefficients increases, the output of approximated periodic signal is more accurate.
A circuit is built to measure the Fourier series of a Square wave
For example, we set s(t) to be square wave with A = 3V, T0 = 0.5*10^-6s The frequency domain of output shown in spectrum analyzer will be:
The time domain of output shown in oscilloscope will be: